Cómo calcular la desviación típica en Excel
La desviación típica es un término estadístico que nos muestra el rango entre la media y los datos reales. Nos permite comprender la variabilidad y la coherencia de los datos. Una desviación típica más alta significa una mayor dispersión, mientras que una desviación típica más baja significa que los datos son coherentes.
Cuando se trabaja con un conjunto de datos numéricos, normalmente se desea saber cuál es el elemento estándar del conjunto. Puede intentar encontrar la media o la mediana, pero la media del conjunto no proporciona información fiable sobre el conjunto.
Media: La suma de todos los individuos dividida por el número de individuos.
Mediana: El individuo que se encuentra en el medio de los ordenados de menor a mayor.
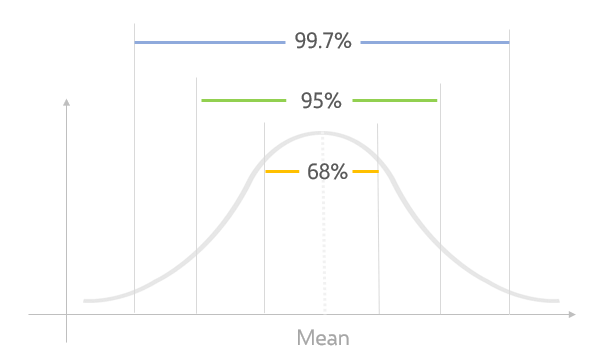
La desviación estándar muestra lo consistentes que son los individuos en este conjunto de datos. Por lo tanto, se utiliza habitualmente y es muy importante.
Lectura recomendada: ¿Cómo normalizar datos en Excel?
Cómo calcular matemáticamente la desviación típica
Permítanos mostrarle cómo calcular la Fecha estándar mediante un ejemplo muy sencillo. Supongamos que tiene un conjunto de datos numéricos: 4, 6, 8, 12, 15.
En primer lugar, debe hallar la media sumando todos los números y dividiéndolos entre el número de individuos del conjunto de datos. En este caso, es 45/5. Por tanto, la media es 9.

A continuación, restamos todos los números de la media y los elevamos al cuadrado para que todos los resultados sean positivos en lugar de negativos. Se sumarán todos estos números elevados al cuadrado entre sí y se dividirán por uno menos del número de individuos de nuestro conjunto de datos (que es 4 en este ejemplo).
Saque la raíz cuadrada de la ecuación y ¡listo! Ha calculado la desviación típica. Es 4.
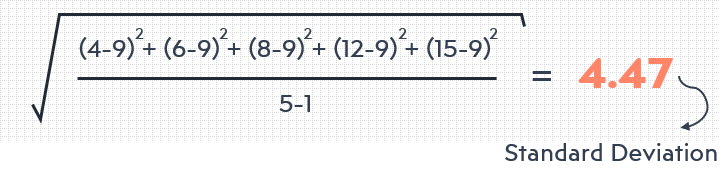
¿Por qué la desviación típica es una estadística importante?
La desviación típica tiene una importancia vital en asuntos como las finanzas. No puede calcular el riesgo teniendo en cuenta únicamente la media. Puede darle una opinión superficial de los datos, pero no es lo suficientemente sana ni informada.
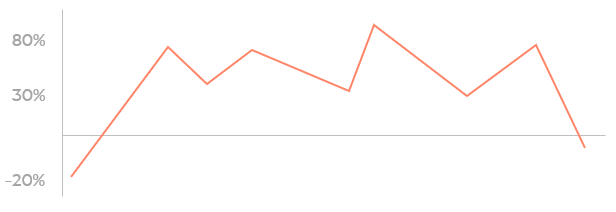
Supongamos que está a punto de invertir algo de dinero en una empresa y le dicen que los inversores recuperan un 30% al final del año. Lo que estos datos le dirán es que la ganancia puede oscilar entre el -20% y el 80%.
Ha solicitado un empleo y le dicen que el salario medio del personal de una empresa es de 20.000 dólares. Esto puede parecer asombroso, pero ¿qué pasaría si los salarios variaran de 1.000 dólares a 19.000 dólares?
Tampoco es posible comparar conjuntos de datos con precisión sin utilizar las desviaciones típicas. Supongamos que tiene dos conjuntos de datos que tienen la misma media. Uno de ellos es 600,30,0 y el otro 299,210,211. Ambos tienen la misma media pero la desviación típica es muy diferente. Mientras que el primer conjunto es poco fiable, el segundo es coherente.
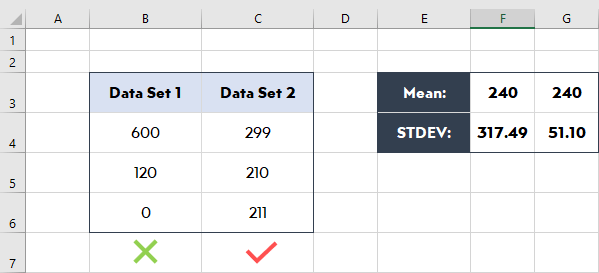
En resumen, la desviación típica es importante porque
- Es un elemento clave para calcular los perímetros de error.
- Nos permite comparar eficazmente dos conjuntos de datos diferentes.
- Nos muestra el riesgo al mostrar el rango de datos
Utilización de la desviación típica en la vida real
En realidad, la gente utiliza esta estadística todos los días en su vida. Le da una opinión realista sobre el rango en nuestro conjunto de datos, por lo que es una fórmula popular. Algunos ejemplos de desviación típica de nuestra vida cotidiana que pueden ayudarle a comprender la importancia de esta estadística:
-
Al calcular el rango respecto a la media en un conjunto de datos:
Una clase de alumnos realiza un examen de física. El profesor descubre que la puntuación media del examen es del 75%. Entonces el profesor decide calcular la desviación típica para ver si las notas se acercan al 75%.
La desviación típica resulta ser muy pequeña y eso significa que las notas de los alumnos estaban muy cerca del 75%.

Una clase de alumnos ha realizado un examen de Lengua y Literatura inglesas. La profesora decide que la nota media del examen es del 55%. Le preocupa que sea muy baja, así que decide calcular la desviación típica para ver cuántos alumnos obtuvieron una puntuación cercana a la media.
La profesora comprueba que la desviación típica es grande. Tras revisar detenidamente todos los exámenes, la profesora es capaz de concluir que numerosos alumnos con puntuaciones muy bajas eran los valores atípicos que arrastraban hacia abajo la media de las puntuaciones de toda la clase.
-
Para encontrar los valores atípicos en un conjunto de datos:
Un veterinario quiere saber si los gatos a su cargo tienen un peso similar o no. Toma el peso medio de los diez gatos (la media).

Después calcula la varianza y, a continuación, la desviación típica. Su desviación típica es notablemente alta. Esto implica que los gatos tienen pesos muy diferentes, o que tiene unos pocos gatos cuyos pesos son valores atípicos que están distorsionando los datos.
-
Mientras determina la fiabilidad de los datos:
Un investigador de una tienda está examinando los resultados de una reciente encuesta a clientes. Quiere tener alguna medida de la fiabilidad de las respuestas dadas en la encuesta para poder predecir cómo podría responder a las mismas preguntas un grupo más amplio de personas. Una desviación típica baja muestra que las respuestas son muy adecuadas para un grupo más amplio de personas.
Otro ejemplo sería el de un meteorólogo cuando analiza la temperatura alta calculada para una serie de fechas frente a la temperatura alta real registrada en cada fecha. Una desviación típica baja mostraría una previsión meteorológica fiable.
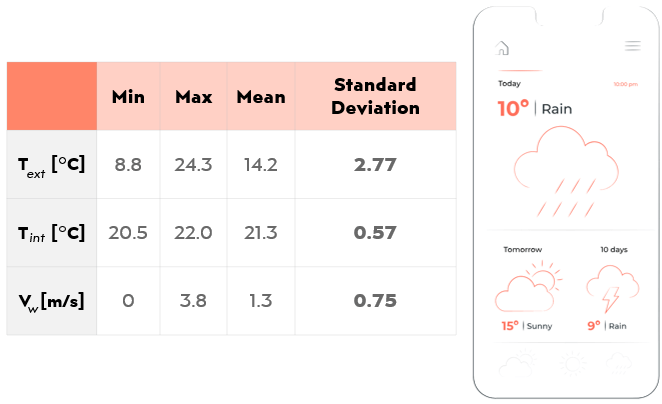
Un empresario quiere determinar si los salarios de un departamento para ver si son justos para todos los empleados, o si hay una gran diferencia. Averigua la media de los salarios de ese departamento y luego calcula la variedad y, a continuación, la desviación típica.
El empresario descubre que la desviación típica es ligeramente superior a lo que esperaba, así que estudia los datos más a fondo y descubre que, aunque la mayoría de los empleados ganan salarios similares, tres empleados antiguos que llevan 15 años o más en el departamento, notablemente más que los demás, ganan mucho más debido a su permanencia en la empresa. Hacer el análisis ayudó al empresario a comprender la gama de salarios de las personas del departamento.
-
Al determinar una medida estándar
En el diseño de la producción, los diseñadores intentan desarrollar sistemas generales de tallaje para determinar las variaciones necesarias en la talla del producto para producir tallas para todo el mundo. Camisas, por ejemplo. O asientos de bebé para coches. Para ello, los diseñadores utilizan la desviación estándar para poder calcular cuánta diferencia deben tener en la línea de productos.
La desviación típica en el deporte
¿Por qué necesitamos estadísticas en los deportes? Piénselo como si fuera el dueño de un equipo:
- Posibilidad de examinar la media de los parámetros de su equipo en los gráficos del panel principal en los que se compara la media estadística de otros equipos de la liga.
- Determine las tendencias al alza y a la baja comparando las estadísticas de su propio partido con las de otros partidos de su elección.
- Poder comparar los datos de su propio partido con los de los partidos de otros equipos para detectar cambios tácticos.
- Poder ver rápidamente los parámetros ofensivos, defensivos, de pase y de uno contra uno del éxito/fracaso de su equipo codo con codo con los ratios de otros equipos.
Los equipos deportivos utilizan la desviación estándar. Por ejemplo, un equipo que tenga un éxito constante puede tener una desviación típica baja, pero un equipo que marque muchos goles puede tener una desviación típica alta.
En los últimos años, el uso de la analítica estadística en los deportes ha ido en aumento. ESPN (plataforma de retransmisión de deportes) incluso ha dedicado un segmento completamente nuevo de su página web a la analítica deportiva. Parece que cada día se desarrollan nuevas métricas para medir el rendimiento de un deportista.
La teoría Moneyball
¿Ha visto la película de Hollywood Moneyball? La película trata de un equipo de béisbol (Oakland A’s) que empieza a utilizar datos para mejorar sus partidos. Es básicamente el comienzo de nuestro mundo deportivo. Hoy en día, atraer a buenos jugadores a los partidos es menos importante que recopilar y procesar los datos. Porque los datos mostrarán a los directivos dónde mejorar, lo que mejorará el juego y las posibilidades de ganar el campeonato (suponiendo que éste sea el objetivo final).
Esta situación acabó creando una teoría llamada La Teoría Moneyball. Da respuesta a dos cosas sencillas: ¿Puede batear el jugador? ¿Puede el jugador crear carreras? Si la respuesta es afirmativa, entonces probablemente su equipo esté en buenas manos.
Este es el método que el director general de los Oakland A’s , Billy Beane, utilizó en 2002. Utilizó la teoría Moneyball para seleccionar un equipo de jugadores infravalorados.

Él y su equipo acabaron ganando 20 partidos seguidos. Entre 2000 y 2006, los A’s de Oakland llegaron a promediar 95 victorias, ganaron cuatro medallas del Oeste de la Liga Americana y llegaron a cinco exhibiciones en los playoffs.
Sólo porque alguien pensó en determinar la desviación típica y procesarla en lugar de conformarse con la media o la observación a simple vista, el mundo del deporte actual cambió por completo.
Descargar gratis: Plantilla para confeccionar el calendario de la liga
Cómo calcular la desviación típica en Excel:
Ahora que ya tiene la información sobre qué es la desviación típica y cómo utilizarla, puede empezar a aprender a calcularla en Microsoft Excel.
Excel es un programa ofimático que nos permite calcular los datos recogidos. Cuenta con herramientas de cálculo, gráficos, tablas dinámicas y un lenguaje de programación de macros llamado Visual Basic para Aplicaciones. Pero puede calcular fácilmente la desviación típica con fórmulas sencillas.
Comencemos.
Existen ocho fórmulas de desviación típica en Excel. Puede calcular la desviación típica de una muestra o de todos los datos que tenga.
Los cálculos muestrales son habituales porque a veces no es posible calcular los datos completos. Y puesto que los cálculos muestrales se utilizan con más frecuencia, empecemos con sus fórmulas.
¿Cómo utilizar STDEV.S o STDEV?
Para utilizar STDEV.S se introduce una fórmula realmente sencilla:
STDEV.S(número1, número2, número3…) o STDEV.S([número1], [número2], [número3],…
Número 1: Es el argumento necesario en la fórmula. Es el primer elemento de la muestra. Puede utilizar una matriz única, un rango con nombre o una referencia a una matriz en lugar de utilizar comas.
Número 2 y número 3: Este es el argumento opcional. Puede añadir hasta 254 argumentos en Excel.
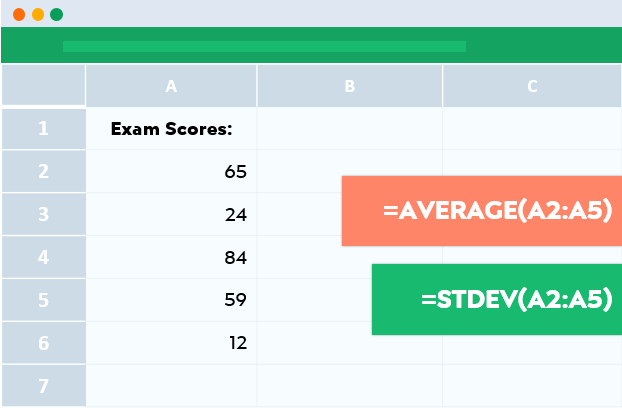
Supongamos que tiene un conjunto de datos de notas de examen de A2 a A11:
Sólo tiene que utilizar la fórmula: =STDEV.S(A1:A11)
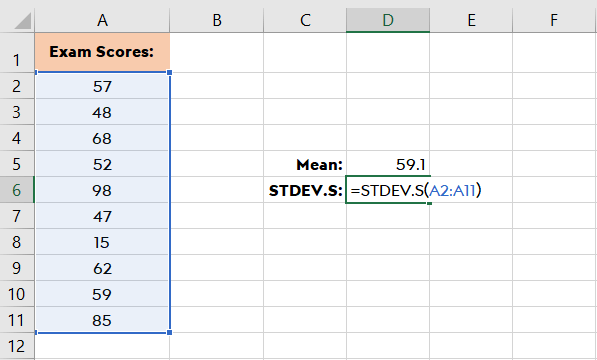
Si tiene una versión anterior de Excel puede utilizar STDEV en lugar de STDEV.S. En el mismo escenario de STDEV.S, se utiliza la fórmula: =STDEV(A2:A11)
Si quiere aprender más sobre las fórmulas de Excel consulte esta hoja de trabajo de Prácticas de Excel.
¿Cómo hacer cálculos de desviación estándar manualmente?
Puede que no se le den bien las fórmulas de Excel o que le resulten demasiado complicadas de utilizar. Siempre puede calcular manualmente sus datos. Veamos cómo hacerlo paso a paso.
Supongamos que ha introducido sus datos de A2 a A11:
Después de introducir sus datos en su hoja Excel debe determinar la desviación. Es decir, el valor menos la media. La fórmula para ello es = A2 -MEDIA($A$2:$A$11). Los valores de las desviaciones se escribirán en la columna B empezando por B2.
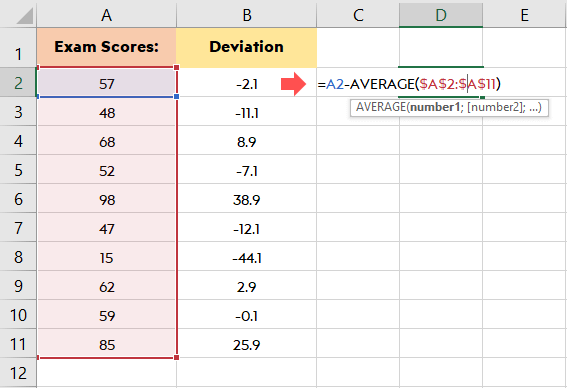
Una vez que calcule la desviación necesitará el valor al cuadrado de sus desviaciones. Así, si tenía valores negativos en los primeros cálculos, todos se convertirán en valores positivos. Para ello, utilizará la fórmula: = (B2)^2. Los valores al cuadrado de la desviación se escribirán en la columna C empezando por C2.

En E3 podrá calcular la desviación típica de la población con esta fórmula:
En E4 puede calcular la desviación típica para una muestra con:
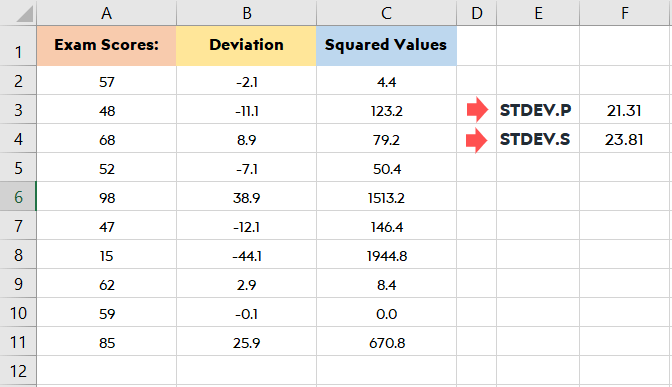
Eso es todo. Puede calcular fácilmente la desviación típica en Excel incluso cuando tenga una gran cantidad de datos. Si quiere saber más cosas que puede hacer con Excel no olvide consultar nuestro artículo Lista completa de cosas que puede hacer con Excel.