¿Cómo calcular el valor P en Excel?
Contenido
¿Qué es el valor P?
El valor P es un término estadístico que le ayuda a determinar, si la hipótesis que utiliza es cierta, la probabilidad de la variación del muestreo. Simplemente nos dice cuáles son las probabilidades de obtener estos resultados si nuestra hipótesis nula es cierta.
- Una hipótesis nula es una hipótesis que afirma que los resultados que obtenemos se deben a la pura suerte.
- Una hipótesis alternativa afirma que los resultados que obtenemos no se deben a la suerte, sino que hay elementos externos que afectan a nuestros resultados.
Se trata de un término estadístico muy importante y de uso común, y puede calcularse fácilmente en programas de análisis de datos como Microsoft Excel. En este artículo, aprenderá cómo la utilizamos, dónde la utilizamos y cómo podemos calcularla en Excel de varias formas.
Comencemos.
¿Por qué necesitamos el valor P?
Cuando se realiza una investigación con grandes poblaciones hay que calcular las estadísticas de cada individuo. Pero incluso en ese caso, no puede estar seguro de si algo ocurre por coincidencia o simplemente por suerte, ya que es imposible observarlo todo. Aquí es donde entra en juego la estadística.
Los cálculos estadísticos no pueden darle una verdad absoluta, pero le ayudarán a tener una buena idea de sus investigaciones.
El valor P nos permite probar la hipótesis sobre nuestro tema. Podemos comparar los resultados matemáticos con estas hipótesis y reconsiderar nuestro camino sin dedicar una gran cantidad de tiempo a la investigación.
¿Dónde utilizamos el valor P en la vida real?
Utilizamos el valor de probabilidad cuando intentamos probar una hipótesis. Puede tratarse de una investigación o de una simple apuesta que hemos hecho con nuestro amigo.
Es más fácil entenderlo con ejemplos.
Marketing:
Supongamos que trabaja en el área de marketing y que su proyecto más reciente es sobre publicidad de cereales.
Ha producido un vídeo para las redes sociales y tiene la información para saber si los usuarios se lo han saltado o lo han visto durante mucho tiempo.
Por ejemplo, el tiempo de visionado común del vídeo es de 20 segundos. La media es de 20 segundos. Y usted ha tomado la decisión de editar el vídeo con un trozo de música más alegre.
Ahora, ¿cómo reconocerá si ha funcionado? En este punto, utilizamos la estadística de significación.
En primer lugar, elabore una hipótesis nula:
Una hipótesis nula afirma que no existe correlación entre lo que invierte y los resultados que obtiene. No afecta a los resultados.
En este ejemplo, la hipótesis nula será la siguiente«No existe ninguna relación entre los cambios que está aplicando y el tiempo del reloj«.
Entonces, la hipótesis alternativa:
La hipótesis alternativa sugiere que el cambio real de la música funcionó y que ahora la gente mira el anuncio durante más de 20 segundos. Matemáticamente, la hipótesis alternativa dice:
«La media es ahora superior a 20 segundos».
Calcule el nivel de significación:
Ahora tenemos que establecer un umbral límite para calcular si tenemos éxito o no. Esto se denomina nivel de significación se denomina adicionalmente valor alfa. Puede ser cualquier porcentaje que desee, depende absolutamente de usted.
Pero en este ejemplo, será 0,05.
Ahora bien, para calcular con certeza deberíamos disponer siempre de todos los datos del tiempo de vigilancia. Pero en lo que respecta a su tiempo y sus fuentes, debería tomar una muestra de la población:
- Usted ha tomado una muestra de 100 personas.
- Estas 100 personas tienen 25 segundos de tiempo de observación del anuncio.
- Esto significa que la media de la muestra es 25.
Esta es una versión muy sencilla del cálculo. Pero la desviación típica de la muestra suele calcularse en esta escala si no conoce la desviación típica de toda la población.
Puede utilizar los valores que calculó para la muestra, ya que se aproximan a los valores de la población. La media de la muestra se aproxima a la media de la población.
Calcule el valor P:
El valor p nos indica si podemos rechazar la hipótesis nula o no. Es la probabilidad de que la media muestral sea mayor o igual a 25 minutos si la hipótesis nula es cierta.
Pueden darse dos situaciones.
- Si el valor p es inferior al alfa puede rechazar la hipótesis nula. Ha obtenido una prueba estadística de que la hipótesis alternativa es cierta.
- Pero si el valor p es mayor o igual que el alfa no podrá rechazar la hipótesis nula. Esto no significa que la hipótesis nula sea ciertamente cierta, pero tampoco se puede evitar.
Probabilidad
Trabajemos con otro ejemplo.
Su amigo y usted lanzan una moneda al aire: Si sale cruz pierdes 5 dólares y si sale cara ganas 5 dólares.
- Suamigo lanza la moneda una vez: sale cruz. No pasa nada, hay un 50% de probabilidades de que salga cruz. Ahora, usted supone que la probabilidad es 0,5 porque cree que es una moneda justa. Esta es su hipótesis nula.
- Segundo: Sale cruz. Ha perdido otros 5 dólares, pero no pasa nada porque sigue habiendo muchas posibilidades de que salgan dos colas seguidas. El valor p es 0,25 y sigue siendo una proporción justa.
- Tercero: sale cruz una vez más. La probabilidad de que haya cruz tres veces seguidas es de 0,12. No es baja, por lo que no hay pruebas suficientes de que la hipótesis nula no sea correcta. Pero usted empieza a pensar que su hipótesis alternativa podría ser correcta.
- Cuarto: Vuelve a salir cruz verá como las probabilidades son cada vez más bajas. Puede ser una coincidencia milagrosa, pero sigue habiendo una probabilidad del 0,6 y todavía no hay pruebas suficientes para apoyar la hipótesis alternativa que dice que la moneda está trucada. Y usted espera al quinto lanzamiento.
- Quinto: sale cruz. La probabilidad de que una moneda salga cruz cinco veces seguidas es de 0,3, lo que es muy bajo. Este es el punto en el que puede rechazar la hipótesis nula porque ya no hay pruebas suficientes para apoyarla.
Le pide a su amigo que vea la moneda y cuando la sostiene se da cuenta de que tiene dos caras cruz y es una moneda trucada.
¿Qué nos hizo perder la fe en nuestra hipótesis nula?
En un juego justo de lanzar monedas, la probabilidad de obtener cara o cruz es del 50%. Esta es una situación en la que creemos que la moneda es justa, pero al bajar el valor p nuestra confianza en esa hipótesis también se debilitó.
Hay pocas posibilidades de obtener cruz al azar cuando el valor p cae por debajo de 0,05. Así que cuando se aplica este término estadístico en asuntos como las investigaciones sobre el cáncer o los efectos del cambio climático cobra más importancia.
Nota: No hay ninguna razón específica por la que utilicemos un valor p de 0,05 para el cálculo por defecto. El creador de la fórmula decidió que era un buen número para calcular y los cálculos por defecto se ciñen a él.
0,05 significa un 5% en poblaciones de 100 individuos que cae dentro de la curva normal. Esta es una de las razones por las que se utiliza habitualmente. Si desea cambiarlo durante el cálculo usted mismo, puede hacerlo.
¿Cómo calcular el valor P en Excel?
Hay más de una forma de calcular el valor p en Microsoft Excel. Puede escribir las fórmulas o puede utilizar Analysis ToolPak. Este artículo contiene cómo hacerlo de ambas formas.
Uso de fórmulas clásicas de Excel:
Empecemos por la forma clásica de utilizar fórmulas de Excel. Hay dos formas de hacerlo: la fórmula TDIST y la fórmula de la prueba T.
1.1) Fórmula TDIST
En primer lugar, necesitará un conjunto de datos para calcular un valor p.
- Supongamos que es usted profesor y quiere comparar la puntuación obtenida por sus alumnos en su último examen y la que esperaba que obtuvieran basándose en sus exámenes anteriores.
- Tiene los resultados 25, 46, 34, 27, 35, 43, 40, 44, 21 y 39 para su último examen.
- Ahora para el cálculo, necesita otra cola, esta es la puntuación que esperaba basándose en exámenes anteriores: 23, 44, 32, 20, 46, 37, 35, 42, 33 y 35
Ahora, para utilizar la fórmula del valor p en Excel, debe calcular algunas cosas de antemano:
Coeficiente de Pearson (r): Es un término estadístico que mide la correlación lineal entre dos datos. No es necesario que conozca su aspecto matemático para calcular el valor p. Verá la fórmula sencilla para ello en los párrafos siguientes.
Población (n): n es el número total de individuos de su conjunto de datos.
Estadística T: Es la relación entre la desviación del valor estimado de los datos respecto a su valor supuesto y su error estándar.
Grado de libertad: Es el número de individuos del conjunto de datos menos dos.
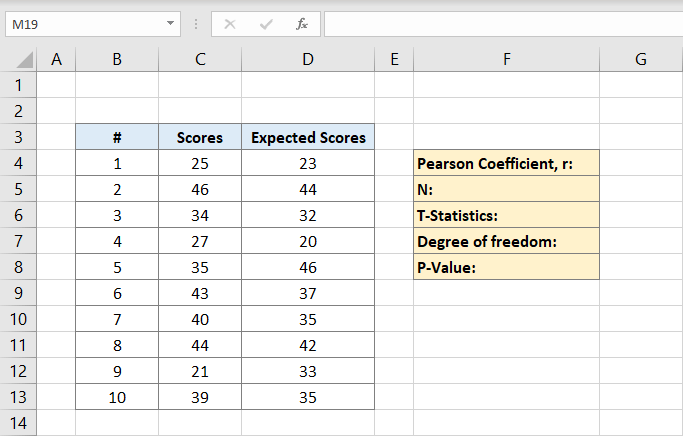
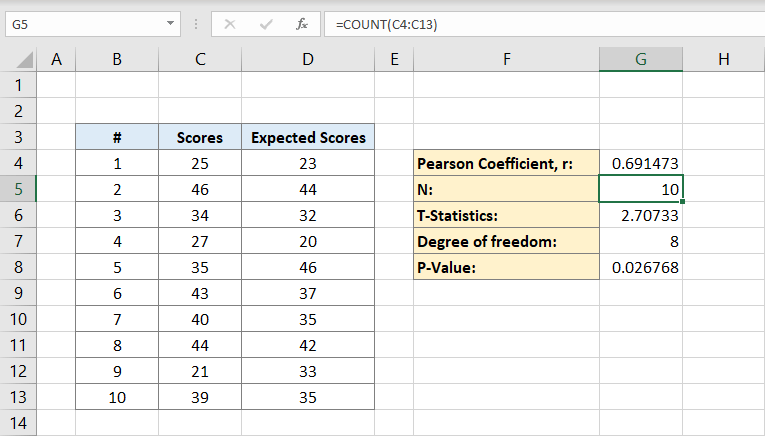
Ahora, el coeficiente de Pearson se escribirá en F4 en este ejemplo. Después de hacer clic en él, escribirá la fórmula:
Las columnas C corresponden a las puntuaciones y las columnas D a las puntuaciones esperadas. El coeficiente de Pearson es 0,691473 en este ejemplo.
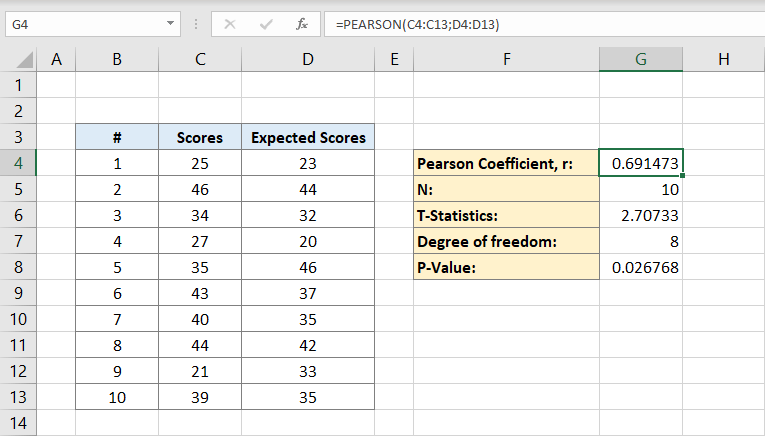
A continuación, teclee el número de individuos del conjunto de datos. Si sabe con certeza cuántos individuos tiene puede escribirlo manualmente, pero si no lo sabe puede utilizar la fórmula:
¿Por qué la fórmula sólo contiene una columna C?
Es porque sólo necesitamos los individuos de un conjunto de datos para realizar el cálculo, por lo que bastará con una columna. La celda G5 contendrá ahora el número 10 en ella. Esta es nuestra población.
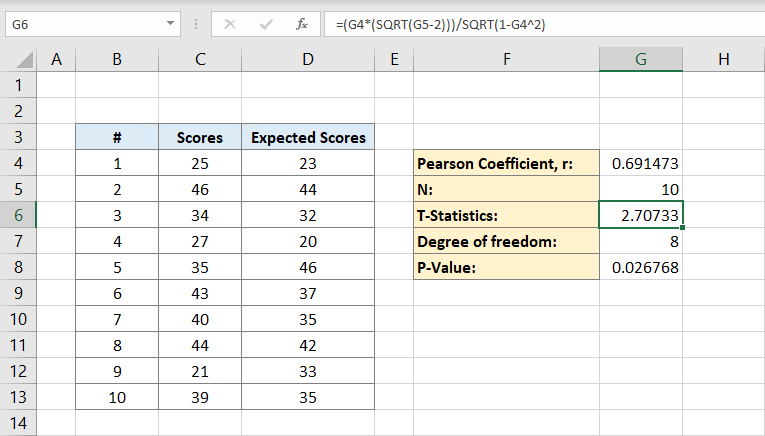
Ahora que tiene tanto el coeficiente de Pearson como la población puede calcular la estadística T. La fórmula matemática para la estadística T es el coeficiente de Pearson (r) multiplicado por el signo de la raíz cuadrada de la población (n) menos 2 dividido por la raíz cuadrada de 1 menos el coeficiente de Pearson al cuadrado:
La celda G6 contendrá el resultado 2,70733. Este es nuestro estadístico T.
A continuación, calculará el grado de libertad. Escribirá
en la celda G7. Este es el grado de libertad. Estará en 8.
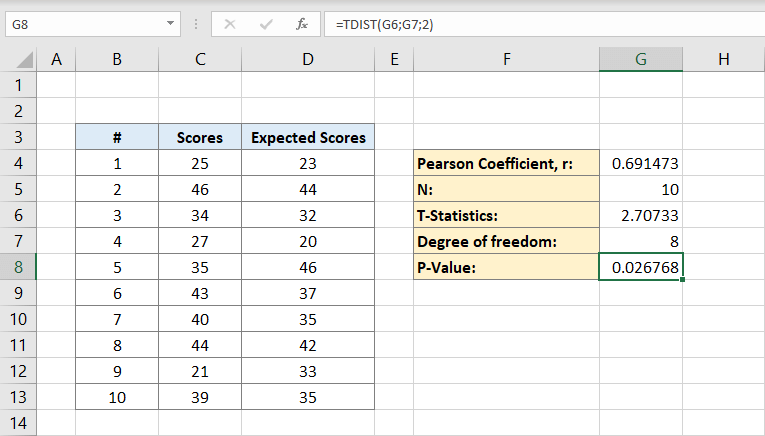
Ahora tiene todo lo que necesita para calcular el valor P. La celda G8 contendrá la fórmula para ello. Es decir
O
El resultado será 0,026768. Este es el valor p para el conjunto de datos.
1.2. Fórmula de la prueba T
La segunda forma de determinar el valor p con fórmulas de Excel es utilizando la fórmula de la prueba T. Es un poco similar al ejemplo anterior pero más corta.
- Supongamos que el conjunto de datos es el mismo, usted tiene los resultados 25, 46, 34, 27, 35,43, 40, 44, 21, 39 para su último examen.
- Los resultados esperados son 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
- Va a añadir una tercera columna para la diferencia entre lo esperado y la puntuación real. En la columna de la diferencia se escribirá 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 de E4 a E13.
Ahora escriba Prueba T en la celda E8. Va a escribir la fórmula de la prueba T en la celda en blanco de al lado. Es decir
Y esta fórmula le dará directamente el valor p.
Determinar el valor p con Excel Tool Pak
Took Pak es un paquete que le permite calcular diversas medidas estadísticas de forma automática, por lo que resulta fácil y muy práctico. También es fácil de instalar.
Paso 1: Vaya a configuración. Hay un botón «Complementos» en la parte inferior izquierda, haga clic en él. Aparecerá una nueva ventana, busque la opción «Analysis Tool Pak», haga clic en ella y, a continuación, haga clic en el botón ir de la parte inferior de la ventana.
Paso 2: Active el complemento haciendo clic en el símbolo de la marca de verificación que aparece junto a él y después en el botón Aceptar de la columna derecha.
Paso 3: Si ha conseguido activarlo correctamente, aparecerá un botón «Análisis de datos» en el menú superior de su hoja de cálculo, a la derecha.
Paso 4: Haga clic en el botón «Análisis de datos» y elija la «Prueba t: Dos muestras pareadas para medias». A continuación, haga clic en Aceptar. Aparecerá una nueva ventana.
Paso 5: Le pedirá las entradas en la primera fila de la ventana. Escriba C4: C13 en la casilla «rango de la variable 1». Teclee D4: D13 en la casilla «rango variable 2». Deje la casilla alfa con su valor por defecto.
Paso 6: En la segunda fila de la ventana puede seleccionar dónde monitorizar sus resultados. Puede ser una nueva hoja de cálculo o cualquier celda en blanco. Si desea el resultado en una celda asegúrese de bloquear la columna y la fila. Después haga clic en el botón Aceptar.
Consejo: Utilice el signo de dólar antes de la letra y el número para bloquear la columna y la fila. Por ejemplo, si desea bloquear la celda A2 escriba $A$2.
Paso 7: El Excel calculará la media, la varianza, las observaciones, la correlación de Pearson, la diferencia de medias hipotética, la estadística t, el valor p, etc.
PALABRAS FINALES
El valor p es fácil de calcular y adaptar en muchas situaciones diferentes. Le ayuda a obtener la información que necesita sin dedicarle mucho tiempo ni esfuerzo. Es incluso más fácil de calcular cuando se utilizan programas de análisis estadístico como Microsoft Excel que vienen con las herramientas y fórmulas adecuadas. Echemos un vistazo a la colección de plantillas de Someka y descarguemos plantillas estadísticas para facilitarle el trabajo.
Lecturas relacionadas: