¿Qué es una matriz de pagos? ¿Cómo usar matrices de pagos para la priorización?

Hoy vamos a descubrir el concepto de matriz de retribución. ¿Qué es una matriz de retribución? ¿Cómo utilizarla para establecer prioridades y tomar decisiones empresariales? Con ejemplos y casos prácticos.

Tabla de contenido

1. ¿Qué es la matriz de retribución?
2. Conceptos clave sobre la matriz de retribución
3. ¿Cómo crear una matriz de retribución?
4. El dilema del prisionero
5. ¿Cómo priorizar las soluciones utilizando una matriz de retribución?
6. Recapitulación de la matriz de retribución
7. Preguntas más frecuentes

La matriz de retribución es una de esas herramientas sólidas, una noción tomada de la teoría de juegos que ha encontrado aplicaciones en diversos sectores como la economía, la estrategia empresarial y la gestión de proyectos. En este post, veremos qué es una matriz de recomp ensa, cuáles son sus elementos principales y cómo puede utilizarse para priorizar con éxito soluciones en entornos complejos.

1. ¿Qué es la matriz de retribución?

Una matriz de retribución es una herramienta utilizada en la teoría de juegos y en la economía para mostrar y analizar los resultados potenciales de diversas acciones estratégicas realizadas por los jugadores.

Es una tabla que muestra las retribuciones (es decir, las ganancias o pérdidas) de cada jugador en función de las estrategias o acciones que elija. Cada celda de la matriz refleja el resultado de una determinada combinación de estrategias, lo que demuestra cómo la retribución de cada jugador se ve influida por las elecciones de todos los jugadores.

La matriz ayuda a prever los resultados más probables de un escenario en el que los responsables de la toma de decisiones son interdependientes, y proporciona un método estructurado para evaluar las interacciones estratégicas en el ámbito empresarial, político o social.

2. Conceptos clave sobre la matriz de retribución

Para comprender la matriz de retribución es necesario familiarizarse con los siguientes conceptos fundamentales:

Jugadores: Son los decisores del escenario, normalmente dos o más, cuyas estrategias interactúan entre sí.

Opciones: Cada participante dispone de un conjunto de estrategias o acciones entre las que puede elegir.

Escenario: Situación o juego específico en el que interactúan los jugadores y que influye en los métodos que pueden emplear.

Estrategia dominante: Una estrategia que, independientemente del plan del adversario, conduce a un final mejor para el jugador.

Equilibrio de Nash: Condición en la que ningún jugador se beneficia de cambiar su estrategia mientras los demás mantienen la suya. Denota un estado de respuestas mutuamente beneficiosas.

Punto de equilibrio: Condición en los juegos de suma cero en la que las estrategias de ambos jugadores dan como resultado el menor pago para uno de ellos y el mayor pago para el otro.

Estos principios son fundamentales para estudiar y comprender la dinámica dentro de una matriz de pagos, permitiendo a los jugadores anticiparse y elaborar estrategias con éxito en diversos escenarios.

3. ¿Cómo crear una matriz de pagos?

Hay varias fases organizadas que intervienen en la creación de una matriz de pagos:

#Paso1: Determinar los jugadores:

Empiece por determinar quiénes son los jugadores del escenario. Una matriz sencilla suele tener dos jugadores.

#Paso2: Haga una lista de las estrategias:

Haga una lista de todas las estrategias o acciones posibles para cada jugador. Éstas deben ser exhaustivas y mutuamente excluyentes.

#Paso3: Cree la disposición de la matriz:

Haga una cuadrícula o tabla con las estrategias de un jugador en las filas y las del otro en las columnas.

#Paso 4: Determine sus resultados:

Determine el resultado o la recompensa para ambos jugadores en cada celda de la matriz, dada la combinación de estrategias elegida. El beneficio, el coste, la utilidad o cualquier otra medida aplicable puede utilizarse para calcular estos payoffs.

#Paso5: Rellene los espacios en blanco de la matriz:

Rellene los pagos de cada combinación de estrategias para completar la matriz. Cada celda debe mostrar el resultado para ambos jugadores.

#Paso6: Examine si hay equilibrio:

Cuando la matriz esté completa, examínela en busca de equilibrios de Nash o estrategias dominantes.

La creación de una matriz de resultados requiere un estudio minucioso de todas las interacciones y resultados potenciales, asegurándose de que la matriz refleja adecuadamente el escenario estratégico que se está debatiendo.

4. El dilema del prisionero

El dilema del prisionero es un ejemplo clásico de la teoría de juegos que demuestra cómo funcionan las matrices de resultados. En este escenario, dos delincuentes son capturados e interrogados individualmente. Deben elegir entre traicionar a su amante y testificar contra ellos o permanecer en silencio. La matriz de pagos de este escenario ofrece cuatro resultados posibles.

• Si ambos reclusos se traicionan, cada uno recibirá un castigo moderado.
• Si ambos guardan silencio, recibirán un castigo leve debido a la falta de pruebas.
• Uno traiciona, el otro permanece mudo: Si uno traiciona y el otro permanece mudo, el traidor queda libre, mientras que el silencioso es condenado a prisión.

Aunque el resultado colectivo óptimo es que ambos permanezcan en silencio, cada prisionero tiene un fuerte incentivo individual para traicionar, lo que da lugar a un resultado menos ideal para ambos.

5. ¿Cómo priorizar las soluciones utilizando una matriz de retribución?

Una matriz de retribución puede ser una herramienta útil para priorizar soluciones en diversas situaciones de toma de decisiones.

En primer lugar enumeramos nuestros pasos sobre cómo puede utilizar las matrices de retribución para establecer prioridades y tomar decisiones empresariales:

1. Establezca el contexto de la decisión: Describa detalladamente la situación o el problema para el que se están priorizando soluciones.
2. Determine las soluciones potenciales: Haga una lista de todas las opciones posibles. Éstas constituirán una dimensión de su matriz (filas o columnas).
3. Establezca los criterios de evaluación: Determine los criterios que utilizará para evaluar cada solución. Estos criterios constituirán la segunda dimensión de su matriz.
4. Asigne valores de pago: Asigne un valor de retribución a cada intersección de una solución y un criterio en su matriz. Este valor debe indicar la eficacia o el beneficio de la solución en relación con el criterio dado.

1. Examine la matriz: Examine la matriz terminada para determinar qué soluciones tienen los mejores beneficios globales en función de sus criterios.
2. Considere diferentes puntos de vista: Si procede, incorpore a la matriz varios puntos de vista de las partes interesadas, lo que puede modificar los valores de las recompensas.
3. Tome decisiones informadas: Utilice las conclusiones de la matriz para elegir las soluciones que ofrezcan las mayores ventajas globales.

En este contexto, la matriz de recompensas fomenta un enfoque organizado y comparativo de la toma de decisiones al garantizar que todas las posibilidades se evalúan cuidadosamente en función de criterios críticos.

Estudio de caso 1 – Establecimiento de prioridades con la matriz de retribución

Este estudio de caso ofrecerá un ejemplo de una empresa que intenta tomar su decisión de marketing.

Escenario: Decisión sobre la estrategia de marketing

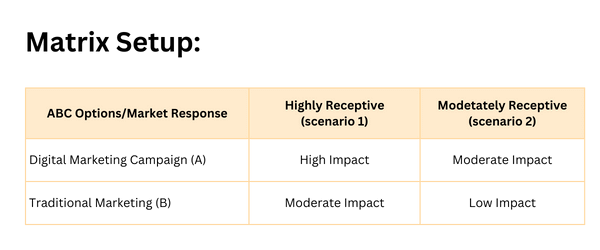
Una pequeña empresa tecnológica emergente, ABC, está decidiendo su estrategia de marketing para el próximo trimestre. La empresa se debate entre dos opciones: una campaña de marketing digital (Opción A) y un enfoque de marketing tradicional que incluya anuncios impresos y en los medios de comunicación (Opción B). La eficacia de cada estrategia depende de la respuesta del mercado, que puede ser muy receptiva (hipótesis 1) o moderadamente receptiva (hipótesis 2).

Opciones:

• Opción A: Campaña de marketing digital
• Opción B: Campaña de marketing tradicional

Configuración de la matriz:

No configuraremos nuestra matriz de pagos:

Matriz de retribuciones:

• Alto impacto: Aumento sustancial del compromiso de los clientes y de las ventas.
• Impacto Moderado: Mejora notable pero no tan significativa como el «Impacto alto».
• Impacto bajo: Mejora mínima del compromiso y las ventas.

Resultados:

Si el mercado es muy receptivo (Hipótesis 1), la Campaña de Marketing Digital (Opción A) tendrá un Impacto Alto, mientras que la Campaña de Marketing Tradicional (Opción B) sólo tendrá un Impacto Moderado. Si el mercado es moderadamente receptivo (Hipótesis 2), la Opción A sigue teniendo un Impacto Moderado, mientras que la Opción B tiene un Impacto Bajo.

Basándonos en la matriz de resultados, la Campaña de Marketing Digital (Opción A) es la estrategia más sólida, ya que conduce a un éxito al menos moderado en ambos escenarios. Por el contrario, la Campaña de Marketing Tradicional (Opción B) corre el riesgo de tener un impacto bajo si el mercado es sólo moderadamente receptivo. TechNovate, por lo tanto, debería considerar dar prioridad a la Campaña de Marketing Digital para su estrategia del próximo trimestre.

Estudio de caso 2 – Rivalidad empresarial con matriz de rentabilidad

Este estudio de caso examinará un caso entre dos coleccionistas de arte.

Escenario: Puja en una subasta

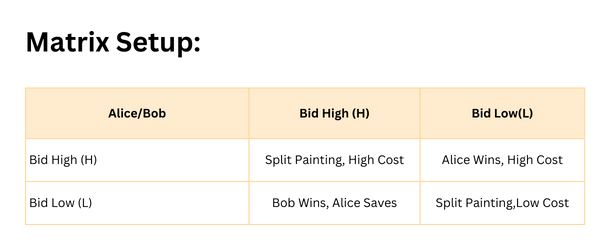
En este escenario, dos coleccionistas de arte rivales, Alice y Bob, pujan por un cuadro raro en una subasta. Tienen dos opciones cada uno: pujar alto (opción H) o pujar bajo (opción L). La suma total de dinero disponible para la puja es constante, y el resultado depende de sus estrategias individuales de puja. La puja más alta gana el cuadro, pero a un coste mayor, mientras que una puja más baja ahorra dinero pero se arriesga a perder el cuadro.

Jugadores:

1. Alice
2. Bob

Opciones para cada jugador:

• Opción H: Puja Alta
• Opción L: Puja baja

Configuración de la matriz:

Así es como podemos crear nuestra matriz de pagos:

Matriz de retribuciones:

• Pintura dividida, coste alto: Ambos jugadores pujan alto y la suma se divide; ambos incurren en costes altos.
• Alice gana, coste alto: Alice puja alto y gana pero a un coste más alto, mientras que Bob ahorra su dinero.
• Bob gana, Alice ahorra: Bob puja alto y gana, Alice ahorra pujando bajo.
• Pintura dividida, coste bajo: Ambos pujan bajo, ninguno gana la pintura, pero ambos ahorran dinero.

Resultados:

• Si tanto Alice como Bob pujan alto (H), se reparten el cuadro pero incurren en costes elevados.
• Si Alice puja alto (H) y Bob puja bajo (L), Alice gana el cuadro con un coste elevado.
• Por el contrario, si Alice puja bajo (L) y Bob puja alto (H), Bob gana el cuadro y Alice ahorra su dinero.
• Si ambos pujan bajo (L), ninguno gana el cuadro, pero ambos ahorran dinero, lo que resulta en un reparto de la suma a un coste bajo para cada uno.

Esta matriz de resultados muestra un juego clásico de suma constante en el que la suma total permanece constante y las elecciones de los jugadores afectan directamente a sus ganancias o pérdidas individuales.

Herramientas de priorización y toma de decisiones

Puede utilizar herramientas de priorización o de elaboración de estrategias para facilitar sus decisiones empresariales. Puede probar las plantillas de estrategia empresarial para ayudarle en sus procesos operativos.

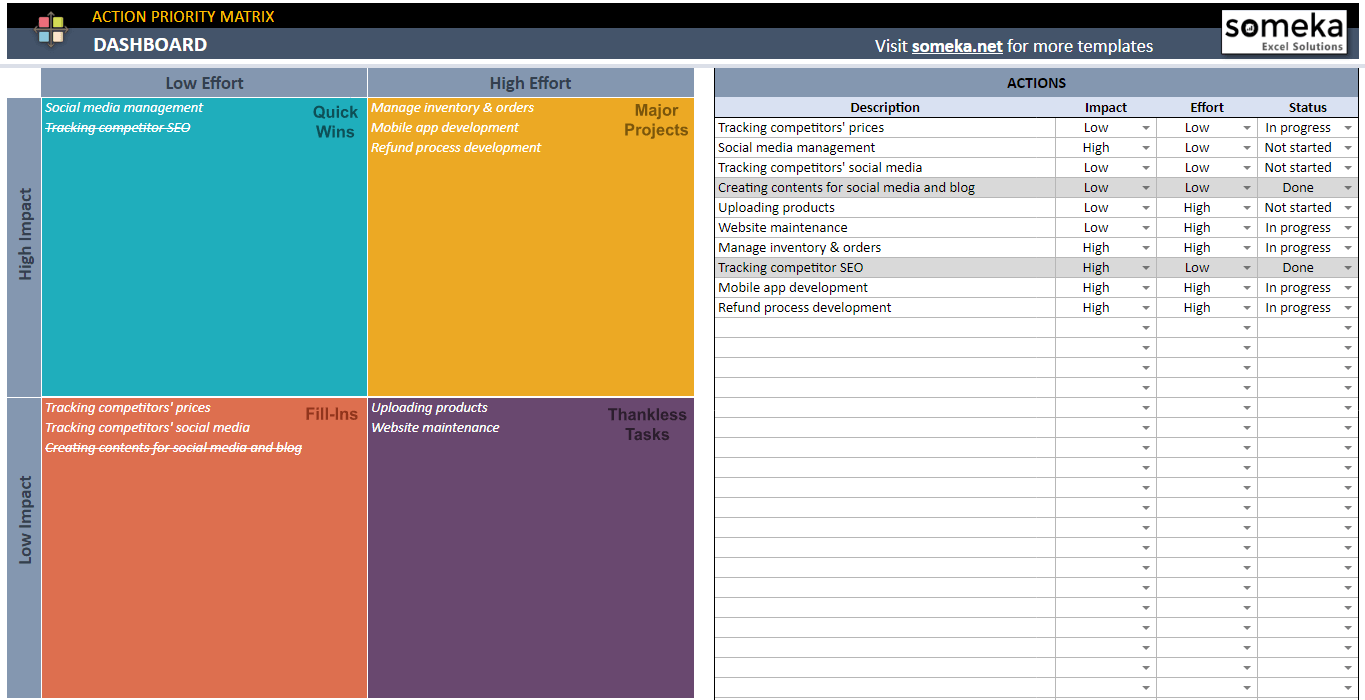
Si busca una solución fácil de usar para priorizar sus tareas diarias, pruebe nuestras herramientas de priotización:

– Esta imagen procede de Action Priority Matrix Google Sheets Template by Someka –

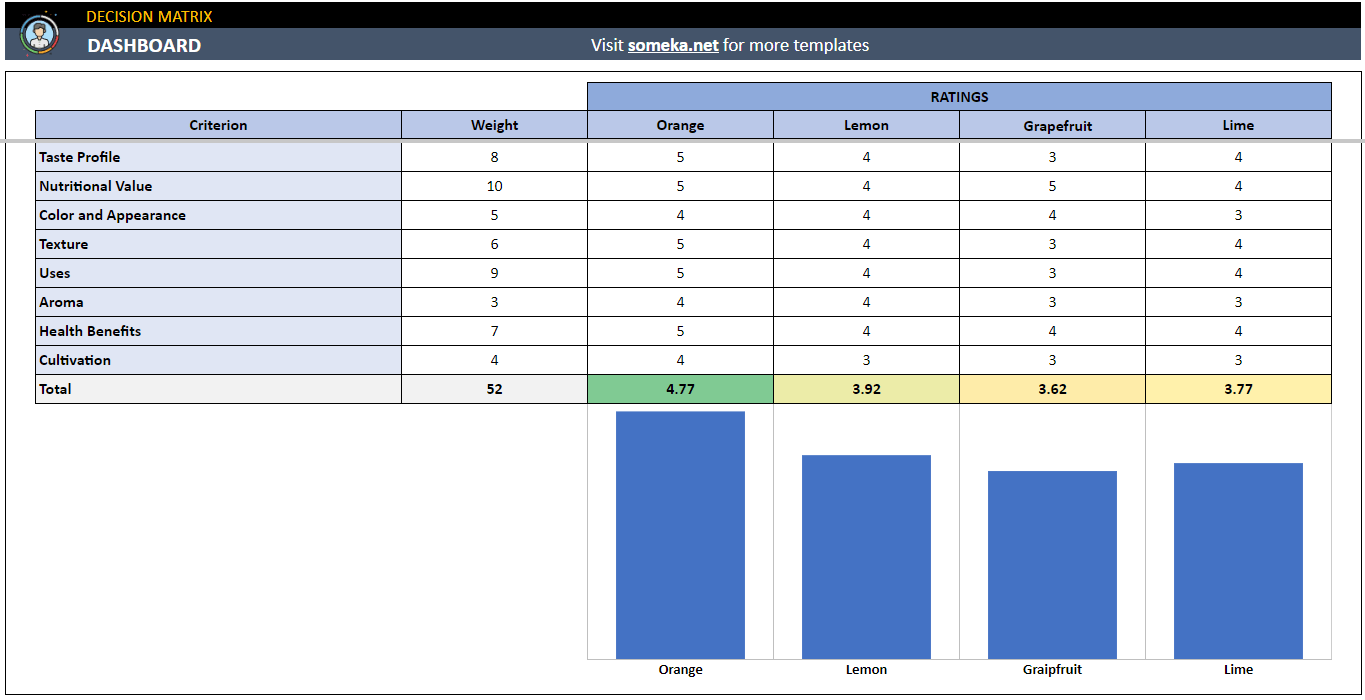
Otra herramienta puede ser nuestra matriz de decisiones:

– Esta imagen proviene de Decision Matrix Google Sheets Template by Someka –

6. Resumen de la matriz de retribución

Por último, la matriz de resultados es una herramienta diversa y sólida en el arsenal de la toma de decisiones estratégicas. Sus aplicaciones abarcan desde la simplificación de problemas complejos de la teoría de juegos, como el Dilema del Prisionero, hasta la ayuda en las elecciones empresariales cotidianas y la priorización de soluciones en una gran variedad de disciplinas.

La eficacia de una matriz de resultados reside en su capacidad para describir y comparar visualmente los resultados de diversas tácticas o acciones, haciendo que las circunstancias complicadas sean más comprensibles y controlables.

7. Preguntas frecuentes

Intentaremos responder a las preguntas más habituales sobre las matrices de pagos.

¿Qué es el resultado final en la teoría de juegos?

Un resultado es la consecuencia o recompensa que un jugador recibe de una acción o estrategia determinada en un juego. Este resultado, que a menudo se cuantifica en términos de utilidad, beneficio u otras medidas relevantes, viene determinado por el conjunto de estrategias elegidas por todos los jugadores del juego.

Los resultados son una parte importante de la teoría de juegos porque ayudan a los jugadores a comprender las consecuencias de sus decisiones y les orientan a la hora de tomarlas. Los jugadores de los juegos estratégicos intentan maximizar sus retribuciones basándose en las estrategias que ellos y los demás utilizan.

¿Cuál es la matriz de retribución de una estructura de mercado?

La matriz de retribución de una estructura de mercado es una herramienta económica utilizada para examinar los resultados de diversas acciones estratégicas realizadas por las empresas dentro de un mercado específico. Muestra cómo las compensaciones (como el beneficio o la cuota de mercado) para cada empresa vienen determinadas por las decisiones estratégicas tomadas por todas las empresas del mercado.

En un mercado oligopolístico, por ejemplo, la matriz podría indicar cómo las diferentes tácticas de fijación de precios utilizadas por las empresas competidoras afectan a sus retribuciones relativas. Esta matriz ayuda a las empresas a prever las consecuencias potenciales de las interacciones competitivas y a elaborar estrategias en consecuencia.

Lecturas recomendadas:

¿Cómo hacer una matriz de decisiones en Excel para tomar mejores decisiones?

Metodología Seis Sigma: Definición y Visión General Completa

Cómo utilizar el Solver de Excel para Programación Lineal: Resolución de Problemas de Optimización