Media ponderada: ¿Qué es? ¿Dónde se utiliza? – Guía completa con ejemplos

En este artículo hablaremos de la idea de la media ponderada. Discutiremos el uso de una media ponderada frente a una media simple, cuándo es apropiado utilizarla y cómo calcular medias ponderadas.

Tras ofrecer una explicación técnica, incluiremos algunos ejemplos cotidianos y relacionados con la empresa.

Tabla de contenido

1. ¿Qué es la media ponderada?
2. ¿Por qué utilizamos la Media Ponderada?
3. Cálculo técnico de las medias ponderadas
4. Aplicaciones de la media ponderada en la vida real
5. Notas finales

Ahora vamos a empezar.

1. ¿Qué es la media ponderada?

El concepto de media ponderada es una medida estadística que calcula la media de valores a los que se asignan distintos niveles de importancia o pesos.

Es crucial porque proporciona una representación más precisa de un escenario en el que no todos los elementos contribuyen por igual.

2. ¿Por qué utilizamos la media ponderada?

Empecemos hablando de qué es una media ponderada y por qué es importante. Demostraremos esta idea con un ejemplo sencillo.

Le mostraremos por qué utilizar una media simple puede producir resultados inexactos con dos ejemplos: uno del mundo empresarial y otro de la vida cotidiana.

Ejemplo de la vida cotidiana para la media ponderada:

Consideremos un estudiante que estudia matemáticas durante ocho horas a la semana, se presenta a ocho exámenes al año y obtiene una nota media de noventa en cada uno de ellos. El mismo estudiante también estudia biología, pero sólo durante una hora a la semana. Sólo se ha presentado a un examen y ha obtenido un cincuenta en él.

Matemáticas: 8 horas/semana – 8 exámenes/año – Puntuación: 90

Biología: 1 hora/semana – 1 examen/año – Puntuación: 50

¿Sumamos simplemente 50 puntos para biología y 90 puntos para matemáticas y dividamos el resultado por dos para obtener 70 al evaluar el rendimiento global del alumno? Esto sería engañoso, ya que se hace mucho más hincapié en las matemáticas en términos de horas y exámenes para los alumnos. El rendimiento real del alumno es superior a 70.

Por otra parte, no podemos afirmar que el rendimiento medio de un alumno sea de 75 si ha obtenido sistemáticamente 50 en los exámenes de matemáticas y 100 en uno de biología.

En consecuencia, inflar el rendimiento real del alumno sería falso. Para obtener una media más exacta en estas situaciones, aplicamos la ponderación, que consiste en multiplicar las matemáticas por el número total de clases o exámenes (aplicando la misma fórmula también a la biología).

Media ponderada en empresariales:

En el ámbito de los negocios, la aplicación de la media ponderada se hace más evidente. Supongamos que una empresa vende dos productos con márgenes de beneficio diferentes. Una media simple de los beneficios de estos productos no reflejaría la verdadera salud financiera de la empresa. Aquí es donde entra en juego la media ponderada, considerando cuánto se vende de cada producto y su respectivo beneficio.

Supongamos que obtiene un beneficio medio de 10 unidades de un producto y de 50 unidades del otro cuando vende ambos. ¿Qué tal si simplemente tomamos la suma de 10 y 50 y la dividimos por dos para obtener el beneficio medio? Eso sería engañoso.

La cantidad vendida de cada producto es importante. Su beneficio medio se acercará más al beneficio del producto vendido con más frecuencia si vende mucho del producto que genera 10 unidades de beneficio pero muy poco del que genera 50 unidades.

En consecuencia, una media simple produciría un resultado inexacto. En estas circunstancias recurrimos a una media ponderada. Evaluamos los valores teniendo en cuenta la cantidad o importancia de cada uno.

La media ponderada en la toma de decisiones:

Curiosamente, nuestro cerebro también aplica el concepto de media ponderada en la toma de decisiones, aunque no nos demos cuenta. Por ejemplo, al elegir un restaurante, diferentes factores como la calidad de la comida, el ambiente y el precio se ponderan en función de las preferencias personales. Un proceso similar ocurre al elegir una casa, donde factores como la proximidad a las carreteras principales o el tamaño de la casa tienen pesos diferentes para cada persona.

Este es un ejemplo fantástico de cómo la media ponderada es algo que nuestro cerebro hace todo el tiempo sin que nos demos cuenta.

Las medias ponderadas las calcula nuestro cerebro. ¿Cómo ocurre algo así?

Imagine que se debate entre comer o no en un restaurante.

Su cerebro tiene en cuenta una serie de aspectos del restaurante, como el coste, la rapidez del servicio, el ambiente y el diseño, y el calibre de la comida. Sin embargo, todos estos factores no tienen la misma importancia para todo el mundo. Para algunas personas, el precio no es tan importante como la calidad de la comida. Para otros, la calidad de la comida puede no ser tan importante como el diseño. Para otra persona, el precio puede ser más importante que otras consideraciones. Como resultado, cada persona tiene un conjunto diferente de factores de ponderación -la importancia relativa de cada factor- a la hora de tomar decisiones.

Por ejemplo, una persona que valore mucho la asequibilidad puede no seleccionar un restaurante que sirva buena comida a un precio elevado. Esto demuestra la utilidad de las medias ponderadas a la hora de tomar decisiones.

De hecho, este es un muy buen ejemplo de ser una media ponderada.

O piense en elegir un apartamento: diferentes personas darán diferentes pesos a distintos factores como el nivel del suelo, el tamaño interior y la proximidad a la carretera principal. Un apartamento que parece ideal para una persona puede no ser tan atractivo para otra si, por ejemplo, su proximidad a la carretera principal -un factor crucial para ellos- tiene una mala puntuación. Como resultado, tendrían una puntuación media ponderada global baja para ese apartamento.

Herramientas de la matriz de decisión:

También hablaremos de cómo nuestro producto Matriz de decisiones, que es una herramienta que utilizamos con frecuencia en la vida cotidiana, es una excelente ilustración de esto.

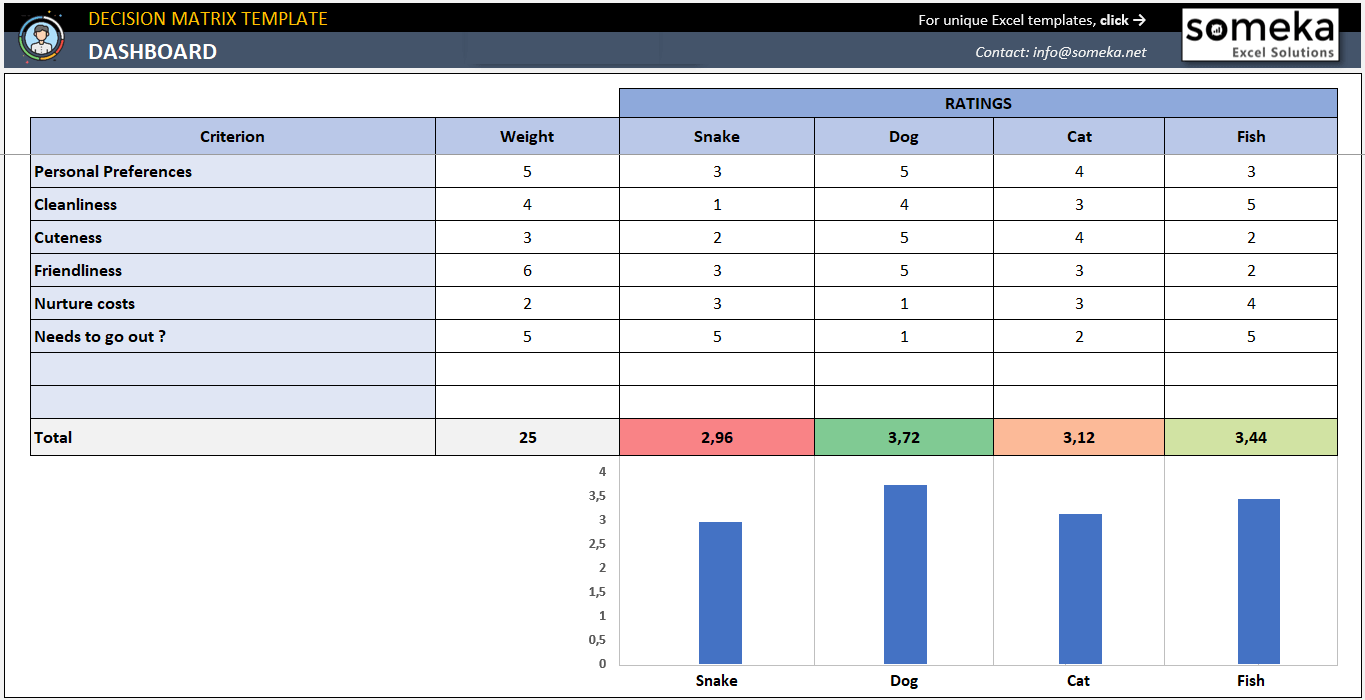
– Este es el cuadro de mandos de nuestra plantilla de matriz de decisión –

Esta plantilla se utiliza para cualquier tipo de decisión. Usted enumera los criterios y luego asigna una puntuación de peso a cada uno de ellos. A continuación, califica cada opción según los criterios. Al final, la plantilla toma las medias ponderadas por usted para ofrecerle la mejor decisión.

3. Cálculo técnico de la media ponderada

Técnicamente, calcular una media ponderada implica multiplicar cada elemento por su peso y sumar estos productos. En Excel, esto puede hacerse utilizando la función SUMPRODUCT.

Analicemos ahora los detalles matemáticos de la creación de una media ponderada.

¿Cómo se calcula una media ponderada en Excel?

Supongamos que tenemos una columna que contiene los siguientes productos: A, B, C, D, etc. Junto a cada producto incluimos una lista de proveedores y sus costes. El producto A puede obtenerse del proveedor 1 por 20 $, el B por 30 $, el C por 5 $ y el D por 10 $. Además, el proveedor 2 tiene precios variables.

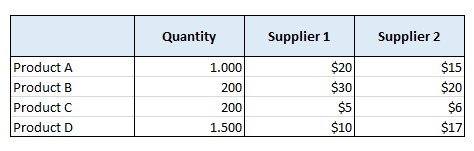
Debemos seleccionar la solución más económica. ¿Cuál es, por término medio, menos cara? El resultado sería incorrecto si nos limitáramos a sumar todos los precios y dividirlos por el número total de productos. Debemos sopesar nuestra información. Importa cuánto pensamos comprar a cada proveedor.

Por ejemplo, el proveedor A puede ser más caro para un artículo pero menos caro para la mayoría de ellos. Incluso con un simple vistazo medio, el proveedor A seguiría pareciendo la mejor opción. Sin embargo, es posible que tengamos la intención de comprar ese único artículo caro en cantidades mayores -digamos 100 unidades- en lugar de las otras 10 unidades. El proveedor B puede salir más beneficiado en esta situación. En un sentido técnico, aquí es donde resulta útil el SUMPRODUCTO.

Para obtener la media ponderada, multiplicamos las cantidades por los precios. Así se realizan los cálculos. El ejemplo siguiente ilustra lo sencillo que es lograrlo en Excel utilizando la función producto suma.

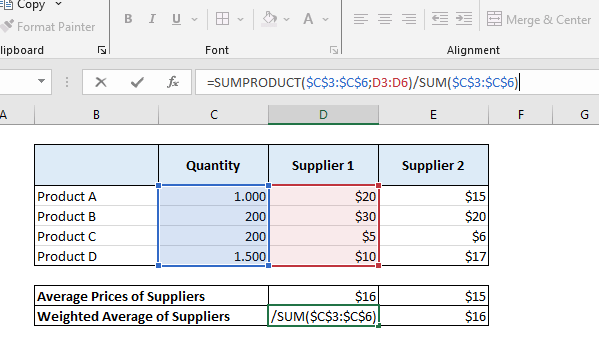
Esto es lo que llamamos una media ponderada. Multiplicamos los valores por el factor de ponderación, es decir, el factor de orientación, y sumamos los resultados y dividimos el número de parámetros. Este es el método de cálculo para ello.

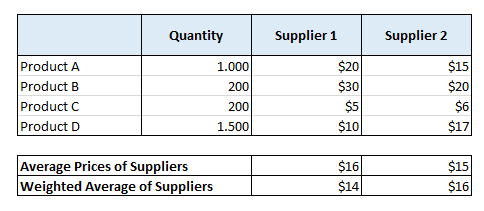
Puede hacerlo muy fácilmente en Excel utilizando la función sumproducto. Como ve, el Proveedor 2 parece más barato cuando sólo comprobamos las medias. Pero en la media ponderada, el Proveedor 1 es mucho más barato.

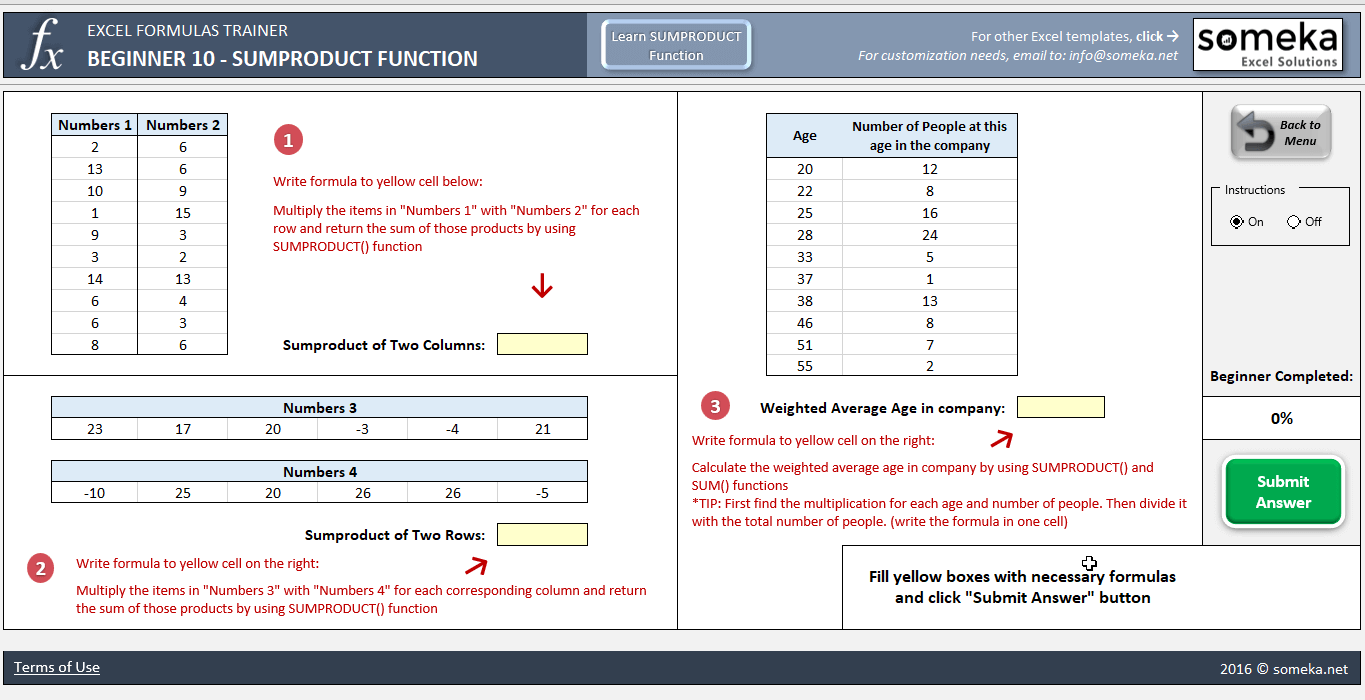
Bonificación:

Si quiere practicar SUMPRODUCTO y otras funciones en Excel, puede descargar nuestro Entrenador de fórmulas de Excel para poner a prueba sus conocimientos de Excel:

4. Aplicaciones reales de la media ponderada

Sí, en la última sección daremos algunos ejemplos de cómo podemos utilizar la media ponderada en el mundo de los negocios.

Ejemplo 1: Análisis de la satisfacción del cliente y clasificación ABC

Es posible ponderar las puntuaciones de satisfacción de los clientes en función del tamaño o la contribución a los ingresos de los distintos segmentos de clientes. Los clientes que interactúan más con su empresa y compran con más frecuencia, por ejemplo, pueden clasificarse utilizando el método de clasificación o segmentación ABC.

Las puntuaciones medias proporcionadas por los consumidores del segmento A pueden considerarse más significativas en este método que las de segmentos inferiores. No tratamos a todos los clientes por igual; los clientes del segmento A, que realizan compras más importantes, reciben puntuaciones más altas. Este método produce resultados más realistas que se ajustan más a nuestros resultados deseados.

Ejemplo 2: Evaluación del rendimiento

La evaluación del rendimiento de los productos es otro ejemplo. En este caso, se puede realizar una evaluación ponderada del rendimiento utilizando el volumen de ventas y los márgenes de beneficio de los distintos productos. Este método hace hincapié en los beneficios de los productos con mayor volumen de ventas, lo que conduce a una representación más precisa del margen de beneficio global de la empresa. Esto se discutió brevemente en la primera sección.

La evaluación del rendimiento de los empleados es otro contexto en el que las medias ponderadas resultan útiles. El rendimiento de los empleados en diversas funciones o departamentos puede ponderarse en función de lo importante que sea el departamento para la empresa. Por ejemplo, supongamos que el departamento financiero tiene 30 empleados y obtiene una puntuación de 5 sobre 5 en cuanto a su impacto en las operaciones de la empresa, mientras que el departamento de calidad, con sólo 2 empleados, obtiene una puntuación de 1.

No podemos limitarnos a decir que la media es de 3. El departamento financiero, al tener más empleados y un mayor impacto en la empresa, debería tener más peso en la evaluación global. Se podría calcular una media ponderada, quizá multiplicando las puntuaciones por el número de empleados de cada departamento. Así, esperaríamos una puntuación más cercana a la del departamento financiero, para una evaluación global más realista.

Ejemplo 3: Evaluar los riesgos

Sí, en realidad podemos terminar el tema dando dos ejemplos más del mundo empresarial. En primer lugar, puede estar relacionado con lo que llamamos gestión de riesgos. Los diferentes factores de riesgo pueden ponderarse en función de su impacto potencial en la empresa, su probabilidad y la magnitud de las pérdidas potenciales.

El factor de ponderación elegido es fundamental en este caso. Por ejemplo, ¿cuánto sufriría la empresa en caso de una inundación, un incendio, una adquisición por parte de la competencia o nuevas normativas gubernamentales que afecten negativamente al negocio?

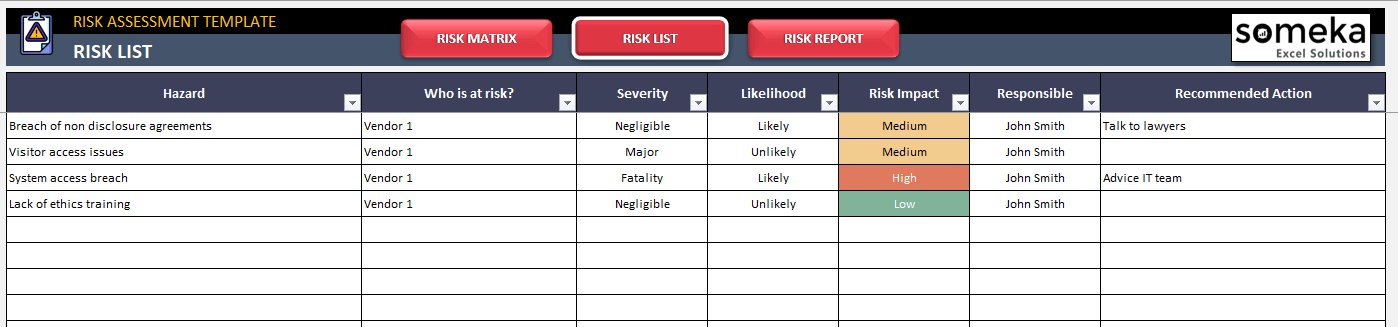
– Esta es la sección Lista de riesgos de la plantilla de evaluación de riesgos de Someka –

Estos escenarios son totalmente independientes, pero sus pesos y probabilidades de ocurrencia difieren. Algunos podrían tener una baja probabilidad de ocurrir pero pueden causar daños moderados, mientras que otros podrían ser más probables y provocar pérdidas significativas. Por lo tanto, es necesario un análisis ponderado.

Ejemplo 4: Análisis de la cuota de mercado

Por último, hablemos del análisis de la cuota de mercado. Las cuotas de mercado de los distintos productos o servicios pueden ponderarse en función de sus ingresos totales o de su número de clientes.

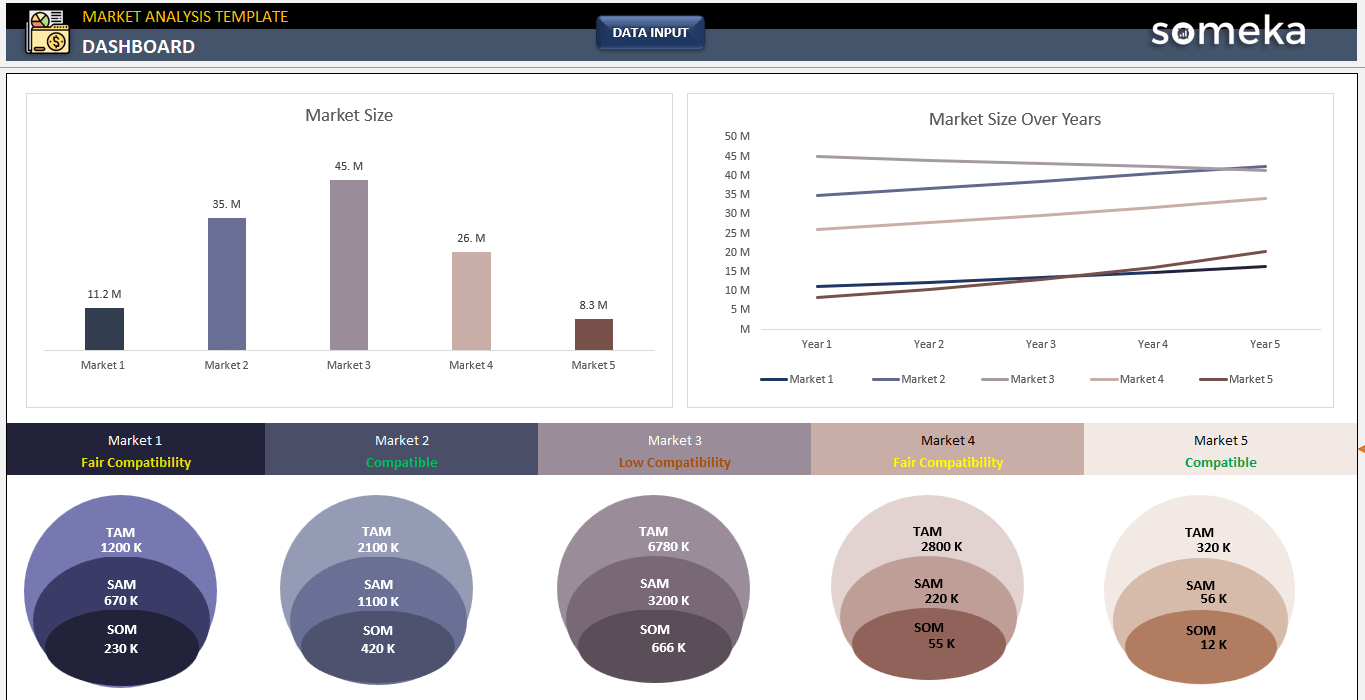
– Este es el cuadro de mando de la plantilla de análisis de mercado de Someka –

Este enfoque permite un análisis más preciso de la cuota de mercado. Por ejemplo, tener una cuota de mercado alta en un grupo de productos menos importante frente a una cuota de mercado baja en un grupo de productos más rentable y con mayores ventas no puede promediarse sin más. Hay que tener en cuenta la importancia de cada grupo de productos a la hora de ponderar.

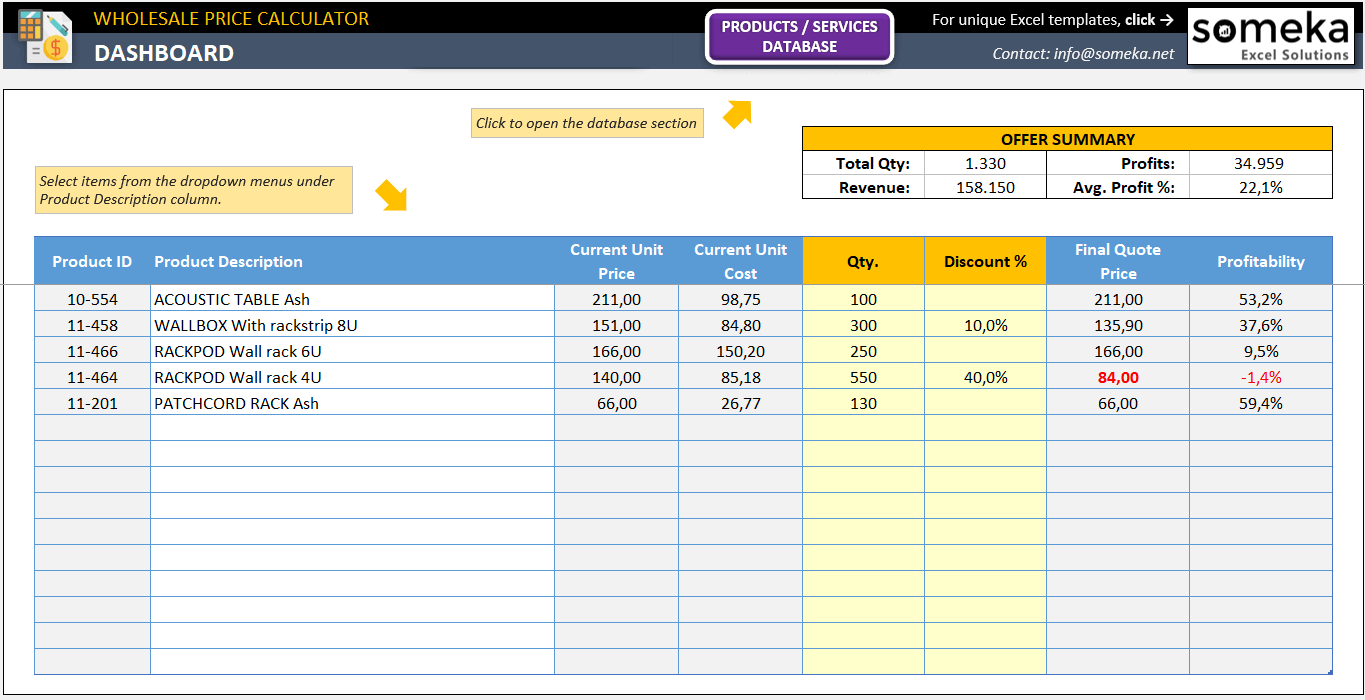
Ejemplo 5: Cálculo del precio al por mayor

Las medias ponderadas también son importantes para calcular los precios al por mayor para los clientes.

– Esta imagen procede de Wholesale Price Calculator by Someka –

Como puede ver en estos ejemplos, lo que llamamos Factor de ponderación y Media ponderada se calculan de esta forma. También puede consultar nuestros productos al respecto.

5. Notas finales

Las medias ponderadas tienen un amplio uso tanto en la vida personal como en los negocios. Incluso en nuestras decisiones diarias nuestro cerebro está continuamente haciendo cálculos de medias ponderadas.

Lecturas recomendadas:

Cómo utilizar la función MEDIA de Excel

Visión general del proceso de evaluación de riesgos: Importancia, pasos y marco

¿Qué es una distribución de Pareto? ¡Aquí tiene una guía reveladora sobre los diagramas de Pareto!