¿Cómo usar el número de Euler en Excel?
El número de Euler, o lo que es lo mismo, el número e, es una de las constantes matemáticas más comunes. Hoy descubriremos cómo utilizar el número de Euler en Excel.
Tabla de contenido
1. ¿Qué es el número de Euler?
2. Breve historia del número de Euler
3. ¿Qué tiene de interesante el número e?
4. ¿Cuál es el significado del número de Euler en matemáticas y matemáticas aplicadas?
5. El número de Euler en las finanzas
6. ¿Cómo utilizar el número de Euler en Excel?
7. ¿Cómo hacer que Excel muestre el número completo en lugar de la e?
8. ¿Cómo utilizar el número de Euler en Python?
9. Conclusión
1. ¿Qué es el número de Euler?
El número de Euler es un número real irracional, llamado así por Leonhard Euler, formulador del número y de sus diversas ecuaciones. Mide aproximadamente 2.718281828459045 y llega hasta el infinito sin repetirse en grandes bloques. También es un número irracional, lo que significa que no se puede escribir en fracciones como 1/2 o 3/4. El número se muestra con una «e» minúscula en matemáticas.
El número de Euler forma parte de nuestras vidas y está contenido en fórmulas y cálculos útiles. Puede que sea más difícil de comprender entre números más famosos como pi o la proporción áurea, pero su misterio hace que merezca la pena aprenderlo y su sentido práctico hace que merezca la pena utilizarlo.
2. Breve historia del número de Euler
Antes de sumergirnos en cómo utilizar el Número de Euler en Excel, revisemos su breve historia. Si no le interesan las raíces de este número mágico, simplemente pase a la parte de cómo hacerlo.
El número de Euler, también conocido como e, tiene una historia tan antigua como la propia civilización. El origen del número se remonta a los matemáticos babilonios. Descubrieron el número pero no pudieron comprender su significado en aquella época.

El número no fue una parte importante de las matemáticas hasta los trabajos de un polímata escocés llamado John Napier. La especialidad de Napier era multiplicar números muy grandes. Los inventos y descubrimientos de su época, en el siglo XVII, requerían trabajar con números grandes y era una tarea ardua porque aún no existían atajos para ello.
Los cálculos duraban páginas y contenían operaciones repetidas. Napier inventó los logaritmos para acortar estos cálculos. El logaritmo permite multiplicar dos números sumando otros dos. Esto significa que es un atajo para demasiadas operaciones de multiplicación.
El número e también se conoce como«número de Napier» en algunos idiomas.
Napier y Bernoulli
El segundo polímata que trabajó sobre el e fue Jacob Bernoulli. Su interés por la e provenía de su interés por las finanzas. Bernoulli trabajaba sobre el crecimiento compuesto. El crecimiento compuesto es la tasa de crecimiento de varios periodos. Para calcularlo Bernoulli utilizó la fórmula tradicional pero era ineficaz al calcular series infinitas y causaba algunos problemas en los principios de salida. Así que añadió e a la fórmula. Fue el primero que escribió e pero el significado del número no se comprendió completamente hasta Euler.

Ahora bien, el número de Euler tiene que ver con el crecimiento, como se ha dicho al principio del artículo. Lo que hizo Leonard Euler con el número fue muy sencillo pero muy eficaz para demostrar su valor. Mostró e como una serie infinita de factoriales. Puede que esté un poco confuso en este punto así que vamos a explicarle lo que esto significa.
Factorial se utiliza con números enteros. Significa simplemente multiplicar los números enteros desde el número escrito hasta 1. Se muestra con un signo de exclamación. Por ejemplo ¡4! significa «4 x 3 x 2 x 1». Del mismo modo 120! significa «120 x 119 x 118 x 117 x … x 2 x 1», etc. Los factoriales se utilizan para mostrarnos de cuántas formas diferentes podemos ordenar algo y de cuántas formas diferentes podemos ordenar la figura dentro de estos grupos ordenados.
Euler formuló este número así:
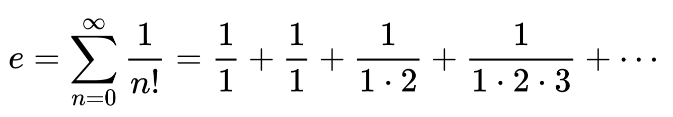
Siendo el número de Euler 2.718281828459045… los primeros términos nos dan el número 2.7166… que se aproxima al número real.
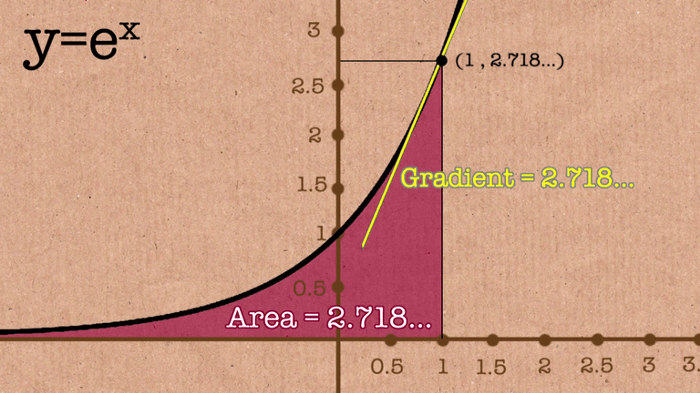
Pero por qué la fórmula llega hasta el infinito. La respuesta es sencilla porque el número va al infinito. El número de Euler nos da el área mostrada en la imagen de abajo y como puede ver su valor disminuye hacia la izquierda pero nunca termina, va hasta el infinito.
3. ¿Qué tiene de interesante el número e?
De acuerdo, Excel es una gran herramienta para utilizar el método de Euler. Pero, ¿qué tiene de especial la constante e?
El número de Euler es la hermana menos famosa de pi.
Al igual que pi, es derivable y llega hasta el infinito. E también está firmemente asociada al crecimiento constante y, por tanto, forma parte inseparable de nuestras vidas. Puede que este número misterioso encierre todavía un secreto que desconocemos.
También hay algunos datos curiosos sobre el número.
Recordar los dígitos del número puede ser difícil de tener en mente. Los matemáticos inventaron un divertido acertijo para tenerlo presente:
Para expresar e recordar memorizar una frase para memorizar esto
Al contar las letras, su lugar en el alfabeto le da el número, y las letras siguientes de las primeras cifras del número.
La misma adivinanza tiene gracia también en francés:
Tu aideras a rappeler ta quantite a beaucoup de docteurs amis
Significa «Ayudarás a recordar tu cantidad a muchos médicos amigos» pero desgraciadamente no da el número de Euler cuando se traduce.
4. ¿Cuál es el significado del número de Euler en matemáticas y matemáticas aplicadas?
El número de Euler es un elemento clave en el crecimiento logarítmico.
He aquí una pregunta matemática para usted:
Usted tiene una cinta de 10 unidades. Tiene que cortarla en trozos y multiplicarlos para obtener el mayor valor posible. ¿Cuántos trozos necesita?
Este parece un problema matemático elemental fácil, pero también es una forma estupenda de mostrar cómo funciona la e.
- Digamos que corta la cinta a 2 y obtiene dos trozos de 5 unidades. Multiplicándolos le da el resultado de 25. Anote el primer resultado.
- Si corta la cinta en 3 trozos, cada trozo medirá 3 1/3 unidades. Multiplicándolos le dará el resultado de 37, 03. Anótelo también.
- Si corta la cinta en 4 trozos, cada trozo medirá 2, 5 unidades de largo, y multiplicándolos obtendrá el resultado de 39, 0625.
- Si corta la cinta en 5 trozos, cada trozo tendrá 2 unidades de longitud, y multiplicándolos dará como resultado 32.
Como puede ver, la longitud máxima se alcanzó al cortar la cinta en 4 trozos.
Si la corta en más o menos trozos no alcanzará el valor óptimo deseado. ¿Qué nos muestra esto? La unidad de longitud más cercana a e, 2,718…, era 2,5, y multiplicar los trozos nos dio el resultado óptimo. El número más cercano a e da el valor más alto y ésta es la magia del número de Euler.
La ecuación más bella del mundo
¿Tiene usted una ecuación favorita? Es una pregunta extraña porque las ecuaciones no se ven como algo que admirar sino como algo que resolver o incluso como una razón para ponerse ansioso si no se lleva bien con las matemáticas.
Antes de repasar el número de Euler en Excel, ¡vamos a divertirnos un poco como frikis!
Algunos matemáticos consideran bellas algunas ecuaciones y la ecuación más bella del mundo es la«identidad de Euler«. Esta ecuación también se conoce como«fórmula de Euler» o«ecuación de Euler«.
Esta fórmula es tan significativa que se compara con los sonetos de Shakespeare o las composiciones de Mozart. Pero, ¿cómo puede ser bella una ecuación?
La ecuación es:
¿Misterio de las matemáticas?
Según Robin Wilson de la Open University del Reino Unido y el profesor David Percy del Instituto de Matemáticas y sus Aplicaciones e incluso el famoso físico Richard P. Feynman, esta ecuación no puede ser superada. Porque contiene el número más misterioso de las matemáticas entre los números base de las matemáticas.
El 0 es el concepto de la nada que es un tema controvertido porque nada es imposible y sin embargo somos capaces de mostrarlo y utilizarlo en matemáticas. Sin el número 0 las matemáticas tal y como las conocemos nunca podrían alcanzar su nivel actual.
El 1 es la base de todos los números. Todos los números enteros positivos son un grupo de este número.
π es otro número misterioso en matemáticas. Simboliza el círculo y el círculo contiene números infinitos e interminables. Además, su valor es aproximadamente 3, 14. Es el cociente de la circunferencia y siempre es el mismo independientemente del tamaño del círculo. El descubrimiento de pi nos ayudó a comprender mejor el mundo porque nos concedió una perspectiva para observar las formas del universo.

i es la raíz cuadrada de menos 1. Es un número imaginario y es significativo porque, en realidad, nada puede ser negativo cuando se multiplica. Por lo tanto, es importante para la base matemática abstracta.
Y por último:
Las ecuaciones contienen fundamentos y misterios de las matemáticas entre tres operaciones matemáticas: suma, multiplicación y exponenciación.
Esta ecuación reúne demasiados términos matemáticos de forma elegante y es comprensible que su nombre se mencione con piezas y formas artísticas.
La ecuación se utiliza para calcular el movimiento de los fluidos, el cálculo, la navegación, la infografía, la robótica, la energía, la dinámica del vuelo, las finanzas y la medicina.
Pero, ¿existe un uso práctico de la ecuación? Por supuesto. Como ya se ha dicho, esta fórmula se utiliza en áreas tecnológicas. También se utiliza para controlar y calcular la corriente alterna. La CA o corriente alterna es el flujo de energía y es lo que hace funcionar el aparato que utiliza para leer este artículo.
5. El número de Euler en finanzas
En este artículo menciono varias veces algo llamado interés compuesto. Es una de las formas más comunes de utilizar el Número de Euler en Excel y también en la vida real.
¿Qué es el interés compuesto?
El interés compuesto es invertir con lo que ha ganado de su interés anterior en el término más simple. O el interés que gana sobre el interés. Crece cada vez más rápido.

¿Cómo se aplica en la inversión y las finanzas?
Veamos este ejemplo:
Supongamos que tiene 1 $ en el banco y que le ofrecen un interés del 100% cada año. Esto significa que al final del año tendrá 2 $.
- ¿Y si le ofrecieran un interés del 50% cada seis meses? ¿Cuánto dinero tendría al final del año? Usted tiene 1 $ y al final de los seis meses, este dinero sería 1,50 $. Y como se trata de interés compuesto al calcular los otros seis meses el interés se tomaría del dinero existente, 1,25 $, y al final del año usted tendría 2,25 $. Esto es más del 100% de interés al año.
- ¿Qué pasaría si el banco ofreciera 1/12 de interés cada mes? Puede calcularlo mes a mes, pero el cálculo formulado sería 1 + (1 + 1/12)12. 1 son sus 1 $ originales. 1 + 1/12 es su crecimiento y la potencia 12 es por cada mes que repita este cálculo. Esto significa que al final del año usted tendría 2, 61 $. Mucho mejor que antes.
- Vamos a calcular el beneficio con 1/52 de interés cada semana. La fórmula que vamos a utilizar es similar a la anterior. 1+ (1 + 1/52)52. Esto es 2,69 al final del año.
- Si tuviera un interés de 1/365 cada día. Su dinero sería de 2, 71 $ al final del año.
La letra n representa el número de periodos del año. Y también puede ver que el total se acerca a la e a medida que aumenta n. Si la n fuera infinita el interés también iría a infinito y nos daría el número de Euler. Euler fue quien lo resolvió mientras trabajaba en el interés compuesto.
6. ¿Cómo utilizar el número de Euler en Excel?
El número de Euler se utiliza en las tasas de crecimiento y, por tanto, en muchos ámbitos. Excel dispone de la fórmula para calcular el valor aproximado de e y sus potencias.
Con esta fórmula, no tendrá que memorizar el valor de e. He aquí cómo funciona la función EXP() en Microsoft Excel.
Su sintaxis es muy sencilla:
El valor se eleva a la potencia del valor. Si teclea 2 donde está escrito valor tendrá e2. O si teclea
tendrá el valor de e+2:
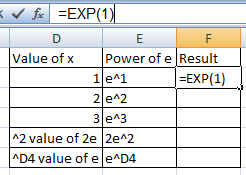
En la primera fórmula el valor es 1 por lo que significa que el resultado es el propio e.
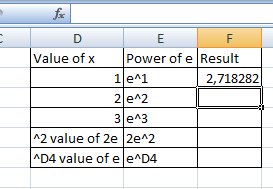
Lo mismo se puede hacer para e2 y e3. Y darán como resultado 7,389056 y 20,08554 en este orden. Otras potencias de la pueden calcularse de la misma manera.
La quinta fórmula señala que también puede utilizar fórmulas y funciones dentro de la sintaxis EXP. En este ejemplo, se da la potencia 2 del valor e de D3. La fórmula para ello debe ser
Se puede escribir cualquier celda rellena en lugar de D3 y la fórmula da el valor de la potencia de la celda escrita.
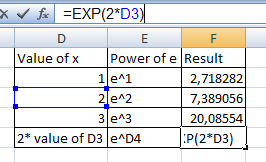
Y entonces obtendrá los resultados:
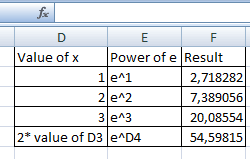
¡Así es como utilizamos el número de Euler en Excel!
7. ¿Cómo hacer que Excel muestre el número completo en lugar de la e?
Cuando hablamos del Número de Euler en Excel, hacer que aparezca un número entero en lugar de e es una de las primeras preguntas que nos hacen los usuarios.
Que Excel muestre «e» en lugar de números completos es en realidad un problema de formato. La mayoría de la gente tiene este problema, sobre todo cuando utiliza conjuntos de datos exportados de bases de datos de terceros. ¿Le resulta familiar también con los archivos CSV? Si es así, continúe para ver cómo deshacerse de este formato de número e:
Por ejemplo: Puede tener un número como 23989488829399488881122334.
Ahora copie esto en una celda, entonces Excel utilizará automáticamente el formato científico:
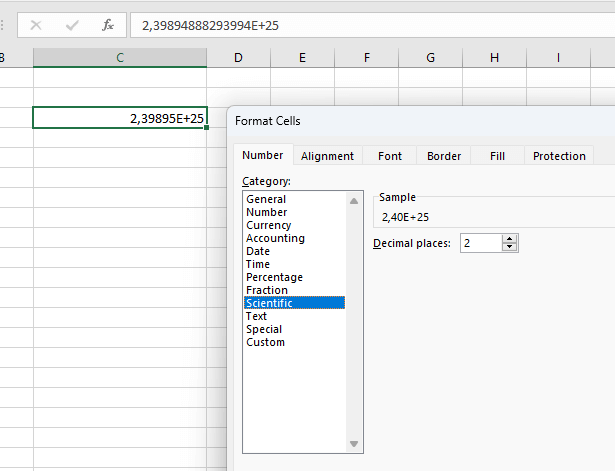
Ahora, simplemente deberá cambiar el formato a Número con cero decimales:
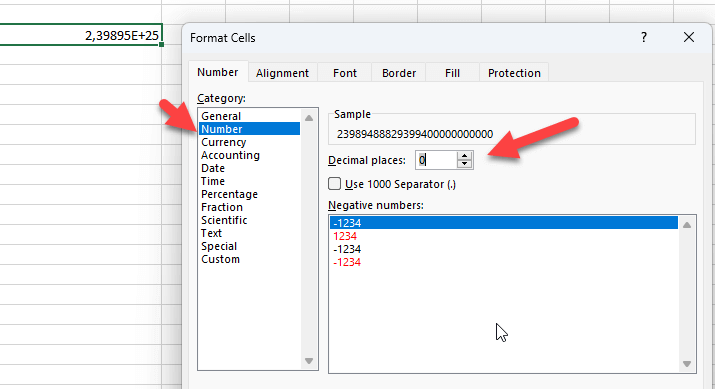
¿Se ve bien? Puede que sí, pero en realidad no. Este método le dará un número diferente del original:
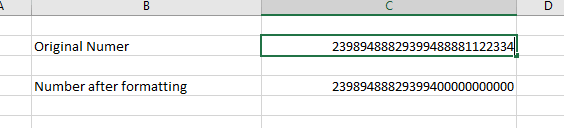
¡Ups! Como hemos mencionado antes se trata de un problema de formato en Excel?
¿Cómo deshacerse de este problema?
Hay una solución: Debe utilizar otro software de hoja de cálculo antes de exportar sus datos a Excel. Pero recuerde que no debe abrir su archivo en Excel en primer lugar. Debe seguir siendo el archivo original.
¡Espero que esto le ayude!
Si quiere mejorar sus conocimientos de Excel, no olvide consultar nuestro Entrenador de fórmulas de Excel: Una herramienta interactiva para practicar las funciones de Excel:
– La herramienta de entrenamiento de fórmulas Excel de Someka proporciona 30 prácticas diferentes en tres niveles –
8. ¿Cómo utilizar el número de Euler en Python?
Python es un lenguaje de programación que puede ejecutarse en varios programas y que se utiliza ampliamente en todo el mundo. Python proporciona el comando matemático para utilizar y calcular e en programación debido al significado del número de Euler.
Para proporcionar una alternativa al número de Euler en Excel, también repasaremos brevemente el uso del número e en el lenguaje Python.
Hay dos formas de alcanzar el valor de e en Python. La primera es el comando«math.e» y la segunda es la función incorporada«exp ()«.
a) Comando math.e de Python
Este comando incluye valores matemáticos como e o pi y es muy utilizado en Python.
Para obtener el valor de e lo primero que tiene que hacer es importar módulos matemáticos. Para ello debe teclear
«Importar math»
en la primera línea.
Lo segundo que hay que hacer es teclear el código para obtener el valor de e. Para ello hay que teclear:
«print (math.e)»
en la segunda línea. El comando «print» permite que el programa ejecute su código.
Ejecutando esto sólo obtendrá el valor de e pero puede calcular más con Python.
Por ejemplo, si escribe
«print (math.e**2)»
O
«print (pow(math.e, 2))»
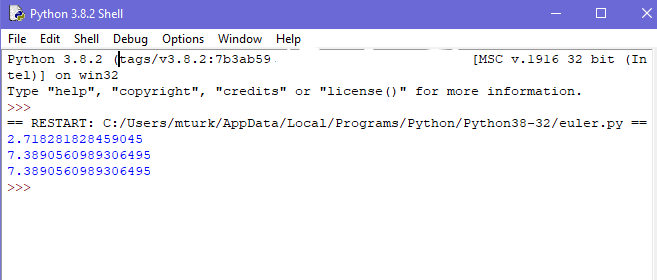
Tendrá el valor de e2. Ambos comandos calculan lo mismo.
b) Función exp () incorporada en Python
Es más precisa que la constante «math.e» según la documentación de Python.
Para utilizarla, tiene que empezar tecleando
«Importar math»
En el primer like. Igual que en el otro ejemplo.
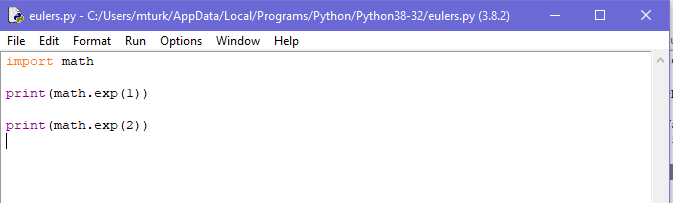
La sintaxis «exp ()» da la potencia del número que desea. Por ejemplo, si desea la potencia de 3 debe escribir «exp (3)». Para tener el valor original del número de Euler, la potencia debe ser 1. Para tener esto debe teclear
«print (math.exp(1)»
Ejecutando esto obtendrá el valor de e. Si desea calcular otros valores como la potencia de e debe teclear:
«print (math.exp(2)»
Ejecutando esto le dará el valor de e2.

Es posible variar estos cálculos. Python tiene una función llamada«evalExp()» que sólo contiene e, números, espacios y símbolos + y -. Esto permite realizar un cálculo sencillo con e.
Por ejemplo, si desea sumar 2 a 5e todo lo que tiene que hacer es teclear:
«print (evalExp(‘5e+2’))»
Y cuando lo ejecute tendrá el resultado de 15, 591409142295225.
9. Conclusión
Como puede ver, el número de Euler es esencial para nuestras vidas y se utiliza en muchas áreas, desde la tecnología a la medicina y desde la física a las finanzas. También es muy fácil de utilizar en matemáticas, lenguajes de programación y Excel. Si intenta evitarlo tendrá que hacer más cálculos, mientras que si lo utiliza según sus necesidades simplificará sus cálculos. Esperamos que disfrute de nuestro artículo sobre el número de Euler en Excel.
Lecturas recomendadas:
Valor P en Excel: ¿Cómo calcularlo?