Excel’de Euler Sayısı Nasıl Kullanılır?

sEuler sayısı, diğer bir deyişle e sayısı, en yaygın matematiksel sabitlerden biridir. Bugün Excel’de Euler Sayısını nasıl kullanacağımızı keşfedeceğiz.

İçerik Tablosu

1. Euler’in sayısı nedir?
2. Euler Sayısının Kısa Tarihçesi
3. E sayısında bu kadar ilginç olan nedir?
4. Euler sayısının matematikteki ve uygulamalı matematikteki önemi nedir?
5. Finans Alanında Euler Sayısı
6. Excel’de Euler Sayısı Nasıl Kullanılır?
7. Excel’de e yerine tam sayı nasıl gösterilir?
8. Python’da Euler Sayısı Nasıl Kullanılır?
9. Sonuç

1. Euler’in sayısı nedir?

Euler sayısı, adını sayıyı ve çeşitli denklemlerini formüle eden Leonhard Euler’den alan irrasyonel bir reel sayıdır. Yaklaşık olarak 2,718281828459045 ‘dir ve büyük bloklar halinde kendini tekrar etmeden sonsuza gider. Aynı zamanda irrasyonel bir sayıdır, yani 1/2 veya 3/4 gibi kesirlerle yazılamaz. Sayı, matematikte küçük harf “e” ile gösterilir.

Euler sayısı hayatımızın bir parçasıdır ve faydalı formüller ve hesaplamalar içerir. Pi sayısı veya altın oran gibi daha ünlü sayılar arasında fark edilmesi daha zor olabilir, ancak gizemi onu öğrenmeye ve pratikliği kullanmaya değer kılmaktadır.

2. Euler Sayısının Kısa Tarihçesi

Excel’de Euler Sayısının nasıl kullanılacağına geçmeden önce, kısa bir tarihçesine göz atalım. Bu sihirli sayının kökleriyle ilgilenmiyorsanız, nasıl yapılacağı kısmına geçebilirsiniz.

Euler’in e olarak da bilinen sayısı, uygarlığın kendisi kadar eski bir tarihe sahiptir. Sayının kökeni Babilli matematikçilere kadar uzanıyor. Sayıyı keşfettiler ama o sırada önemini anlayamadılar.

John Napier adında İskoç bir polimatın çalışmalarına kadar bu sayı matematiğin büyük bir parçası değildi. Napier’in uzmanlık alanı çok büyük sayıları çarpmaktı. Onun zamanındaki, 17. yüzyıldaki icatlar ve keşifler büyük sayılarla çalışmayı gerektiriyordu ve bu zor bir işti çünkü henüz bunun için bir kestirme yol yoktu.

Hesaplamalar sayfalar uzunluğundaydı ve tekrarlanan işlemler içeriyordu. Napier bu hesaplamaları kısaltmak için logaritmayı icat etti. Logaritma, iki sayıyı başka iki sayı ekleyerek çarpmanızı sağlar. Bu, çok fazla çarpma işlemi için bir kısayol olduğu anlamına gelir.

E sayısı bazı dillerde“Napier sayısı” olarak da bilinir.

Napier ve Bernoulli

e üzerinde çalışan ikinci polimat Jacob Bernoulli‘dir. Onun e’ye olan ilgisi finansa olan ilgisinden kaynaklanıyordu. Bernoulli bileşik büyüme üzerinde çalışıyordu. Bileşik büyüme, birden fazla dönemin büyüme oranıdır. Bunu hesaplamak için Bernoulli geleneksel formülü kullandı, ancak sonsuz serileri hesaplarken etkisizdi ve çıktı ilkelerinde bazı sorunlara neden oldu. Bu yüzden formüle e’yi ekledi. E’yi ilk yazan oydu ancak sayının önemi Euler’e kadar tam olarak anlaşılamadı.

Şimdi Euler’in sayısı, makalenin başında belirtildiği gibi büyüme ile ilgilidir. Leonard Euler ‘in bu sayı ile yaptığı şey çok basit ama değerini göstermek için çok etkiliydi. E’yi sonsuz faktöriyel serisi olarak gösterdi. Bu noktada kafanız biraz karışmış olabilir, bu yüzden bunun ne anlama geldiğini açıklayalım.

Faktöriyel tam sayılarla kullanılır. Basitçe, yazılan sayıdan 1’e kadar olan tam sayıların çarpılması anlamına gelir. Ünlem işareti ile gösterilir. Örneğin 4! “4 x 3 x 2 x 1” anlamına gelir. Aynı şekilde 120! “120 x 119 x 118 x 117 x … x 2 x 1” vb. anlamına gelir. Faktöriyeller bize bir şeyi kaç farklı şekilde düzenleyebileceğimizi ve bu düzenlenmiş gruplar içinde şekli kaç farklı şekilde düzenleyebileceğimizi göstermek için kullanılır.

Euler bu sayıyı şu şekilde formüle etmiştir:

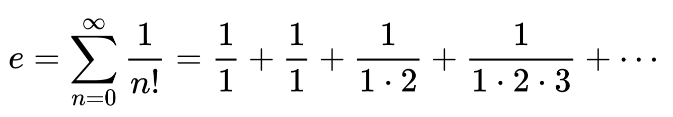
Euler’in sayısı 2,718281828459045… ilk birkaç terim bize 2,7166 sayısını verir… bu da gerçek sayıya yakındır.

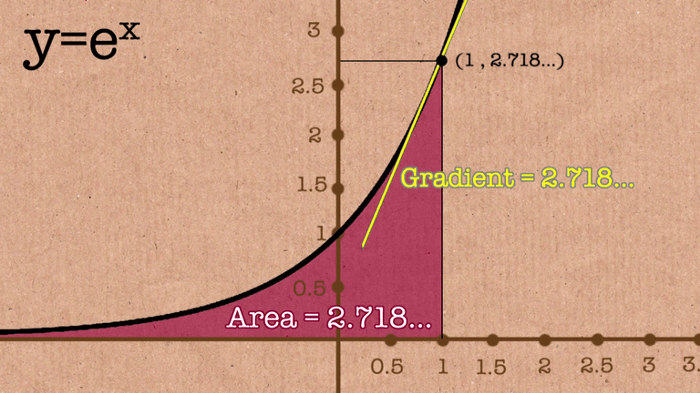
Ama formül neden sonsuza gidiyor. Cevap basit çünkü sayı sonsuza gidiyor. Euler’in sayısı bize aşağıdaki resimde gösterilen alanı verir ve gördüğünüz gibi değeri sola doğru azalır ama asla bitmez, sonsuza gider.

3. E rakamında bu kadar ilginç olan nedir?

Tamam, Excel Euler yöntemini kullanmak için harika bir araç. Peki bu e-sabitin özelliği nedir?

Euler’in sayısı pi’nin daha az ünlü kız kardeşidir.

Tıpkı pi sayısı gibi, türetilebilir ve sonsuza kadar gider. E aynı zamanda istikrarlı büyüme ile sıkı sıkıya ilişkilidir ve bu nedenle hayatımızın ayrılmaz bir parçasıdır. Bu gizemli numara henüz bilmediğimiz bir sırrı içeriyor olabilir.

Sayı hakkında birkaç eğlenceli gerçek de var.

Sayının rakamlarını hatırlamak akılda tutmak zor olabilir. Matematikçiler bunu akılda tutmak için eğlenceli bir bilmece icat ettiler:

Bunu ezberlemek için bir cümleyi hatırlamayı ifade etmek için

Harfleri saydığınızda, alfabedeki yerleri size sayıyı ve sayının ilk birkaç basamağından sonraki harfleri verir.

Aynı bilmece Fransızca’da da zarif bir şekilde mevcuttur:

Tu aideras a rappeler ta quantite a beaucoup de docteurs amis

“Birçok doktor arkadaşınıza sayınızı hatırlamanıza yardımcı olacaksınız” anlamına gelir, ancak ne yazık ki tercüme edildiğinde Euler sayısını vermez.

4. Euler sayısının matematik ve uygulamalı matematikteki önemi nedir?

Euler sayısı logaritmik büyümede kilit bir unsurdur.

İşte size bir matematik sorusu:

Elinizde 10 birimlik bir kurdele var. Onu parçalara ayırmanız ve elde edebileceğiniz en yüksek değeri elde etmek için bunları çarpmanız gerekiyor. Kaç parçaya ihtiyacınız var?

Bu kolay bir ilköğretim matematik problemi gibi görünse de e’nin nasıl çalıştığını göstermek için harika bir yoldur.

• Diyelim ki kurdeleyi 2’ye kestiniz ve 5 birimlik iki parça elde ettiniz. Bunları çarptığınızda 25 sonucunu elde edersiniz. İlk sonucu yazın.
• Eğer kurdeleyi 3 parçaya bölerseniz her parça 3 1/3 birim uzunluğunda olacaktır. Bunları çarptığınızda 37, 03 sonucunu elde edersiniz. Bunu da not edin.
• Eğer kurdeleyi 4 parçaya bölerseniz, her bir parça 2,5 birim uzunluğunda olacaktır ve bunları çarparsanız 39,0625 sonucunu elde edersiniz.
• Kurdeleyi 5 parçaya bölerseniz, her parça 2 birim uzunluğunda olacaktır ve bunları çarparak 32 sonucunu elde edersiniz.

Gördüğünüz gibi kurdeleyi 4 parçaya böldüğünüzde maksimum uzunluğa ulaşıldı.

Daha fazla veya daha az parçaya bölerseniz, istediğiniz optimum değere ulaşamazsınız. Bu bize ne gösteriyor? e, 2,718…’e en yakın birim uzunluk 2,5 idi ve parçaları çarpmak bize optimum sonucu verdi. E’ye en yakın sayı daha yüksek değeri verir ve bu Euler sayısının sihridir.

Dünyanın En Güzel Denklemi

Favori bir denkleminiz var mı? Bu garip bir soru çünkü denklemler hayranlık duyulacak bir şey olarak değil, çözülmesi gereken bir şey olarak görülüyor ve hatta matematikle aranız iyi değilse endişelenmeniz için bir neden olarak görülüyor.

Excel’de Euler sayılarını incelemeden önce, biraz inek eğlencesi yapalım!

Bu yüzden bazı matematikçiler bazı denklemlerin güzel olduğunu düşünür ve dünyanın en güzel denklemi“Euler’in özdeşliği“dir. Bu denklem“Euler formülü” veya“Euler denklemi” olarak da bilinir.

Bu formül o kadar önemlidir ki; Shakespeare’in soneleri veya Mozart’ın besteleriyle karşılaştırılır. Ama bir denklem nasıl güzel olabilir?

Denklem şöyle:

Matematiğin gizemi mi?

İngiltere’deki Açık Üniversite’den Robin Wilson, Matematik ve Uygulamaları Enstitüsü’nden Profesör David Percy ve hatta ünlü fizikçi Richard P. Feynman’a göre bu denklemin üstüne çıkılamaz. Çünkü matematiğin temel sayıları arasında matematiğin en gizemli sayısını içerir.

0, tartışmalı bir konu olan hiçlik kavramıdır çünkü hiçbir şey imkansız değildir ancak biz bunu matematikte gösterebiliyor ve kullanabiliyoruz. 0 rakamı olmasaydı, bildiğimiz matematik asla bugünkü seviyesine ulaşamazdı.

1 tüm sayıların tabanıdır. Tüm pozitif tam sayılar bu sayının bir grubudur.

π matematikteki bir başka gizemli sayıdır. Daireyi sembolize eder ve daire sonsuz, bitmeyen sayıları içerir. Ayrıca değeri yaklaşık olarak 3, 14’tür. Çevrenin oranıdır ve dairenin boyutundan bağımsız olarak her zaman aynıdır. Pi sayısının keşfi dünyayı daha iyi anlamamıza yardımcı oldu çünkü bize evrendeki şekillere bakmamız için bir perspektif sağladı.

i, eksi 1’in kareköküdür. Bu hayali bir sayıdır ve önemlidir çünkü gerçekte hiçbir şey çarpıldığında negatif olamaz. Bu nedenle soyut matematiği temel almak önemlidir.

Ve son olarak:

Denklemler, matematiğin üç işlemi olan toplama, çarpma ve üs alma işlemlerinin temellerini ve gizemlerini içerir.

Çok fazla matematiksel terimi zarif bir şekilde bir araya getiren bu denklemin adının sanat eserleri ve formlarla birlikte anılması anlaşılabilir bir durumdur.

Denklem, sıvıların hareketini hesaplamak, hesap, navigasyon, bilgisayar grafikleri, robotik, enerji, uçuş dinamikleri, finans ve tıp için kullanılır.

Peki bu denklemin pratik bir kullanımı var mı? Elbette var! Yukarıda belirtildiği gibi bu formül teknoloji alanlarında kullanılmaktadır. Ayrıca AC‘yi kontrol etmek ve hesaplamak için de kullanılır. AC veya alternatif akım enerji akışıdır ve bu makaleyi okumak için kullandığınız cihazı çalıştıran şey de budur.

5. Finans Alanında Euler Sayısı

Bu makalede birkaç kez bileşik faiz denen bir şeyden bahsettim. Bu, Euler Sayısını Excel’de ve gerçek hayatta kullanmanın en yaygın yollarından biridir.

Bileşik faiz nedir?

Bileşik faiz en basit tabirle bir önceki faizinizden kazandıklarınızla yatırım yapmaktır. Ya da faizden kazandığınız faizdir. Gittikçe daha hızlı büyüyor.

Yatırım ve finans alanında nasıl uygulanır?

Şu örneğe bakalım:

Diyelim ki bankada 1 dolarınız var ve size her yıl %100 faiz teklif ediyorlar. Bu, yıl sonunda 2 $’a sahip olacağınız anlamına gelir.

• Her altı ayda bir %50 faiz alsaydınız ne olurdu? Yıl sonunda ne kadar paranız olurdu? 1 $’ınız var ve altı ayın sonunda bu para 1,50 $ olurdu. Ve diğer altı ay hesaplanırken bileşik faiz olduğu için faiz mevcut paradan, 1,25 $’dan alınacak ve yıl sonunda 2,25 $’ınız olacaktı. Bu, bir yılda %100’den fazla faiz demektir.
• Banka her ay 1/12 faiz teklif ederse ne olur? Bunu ay ay hesaplayabilirsiniz, ancak bunun için formüle edilmiş hesaplama 1 + (1 + 1/12)12 olacaktır. 1 orijinal 1 $’ınızdır. 1 + 1/12 büyümenizdir ve 12 gücü bu hesaplamayı tekrarladığınız her ay içindir. Bu, yıl sonunda 2, 61 $’a sahip olacağınız anlamına gelir. Öncekinden çok daha iyi.
• Her hafta 1/52 faiz ile karı hesaplayalım. Kullanacağımız formül öncekine benzer. 1+ (1 + 1/52)52. Bu da yıl sonunda 2,69 eder.
• Eğer her gün 1/365 faiz alsaydınız. Paranız yıl sonunda 2,71 $ olacaktır.

n harfi yıl içindeki dönem sayısını temsil eder. Ayrıca n arttıkça toplamın e’ye yaklaştığını da görebilirsiniz. Eğer n sonsuz olsaydı faiz de sonsuza giderdi ve bu da bize Euler’in sayısını verirdi. Euler, bileşik faiz üzerinde çalışırken bunu çözen kişiydi.

6. Excel’de Euler Sayısı Nasıl Kullanılır?

Euler sayısı büyüme oranlarında ve dolayısıyla birçok alanda kullanılır. Excel, e’nin yaklaşık değerini ve kuvvetlerini hesaplamak için bir formüle sahiptir.

Bu formülle, e değerini ezberlemek zorunda kalmayacaksınız. EXP() işlevinin Microsoft Excel’de nasıl çalıştığı aşağıda açıklanmıştır.

Bunun sözdizimi çok basittir:

Değer, değerin gücüne yükseltilir. Değerin yazılı olduğu yere 2 yazarsanız e2 elde edersiniz. Ya da yazarsan:

E+2 değerine sahip olacaksınız:

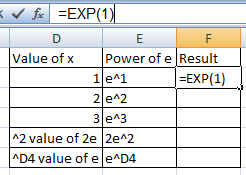
İlk formülde değer 1’dir, bu da sonucun e’nin kendisi olduğu anlamına gelir.

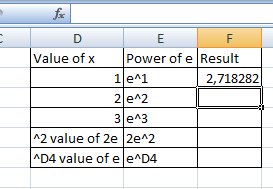
Aynı şey e2 ve e3 için de yapılabilir. Ve bu sırayla 7,389056 ve 20, 08554 sonuçlarını verecektir. ‘nin diğer güçleri de aynı şekilde hesaplanabilir.

Beşinci formül, EXP sözdizimi içinde formüller ve işlevler de kullanabileceğinizi gösterir. Bu örnekte, D3’ün e değerinin 2 kuvveti verilmiştir. Bunun formülü şu olmalı:

D3 yerine herhangi bir dolu hücre yazılabilir ve formül yazılan hücrenin gücündeki değeri verir.

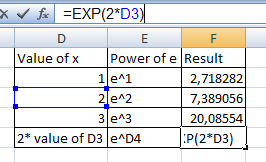
Ve sonra sonuçları alacaksınız:

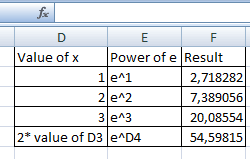
Excel’de Euler Sayısını bu şekilde kullanırız!

7. Excel’in e yerine tam sayı göstermesini nasıl sağlarım?

Excel’de Euler Sayısından bahsettiğimizde e yerine tam sayı yapmak kullanıcılardan gelen ilk sorulardan biridir.

Excel’in tam sayılar yerine “e” harfini göstermesi aslında bir biçimlendirme sorunudur. Çoğu kişi, özellikle üçüncü taraf veritabanlarından dışa aktarılan veri setlerini kullanırken bu sorunu yaşar. CSV dosyaları da size tanıdık geliyor mu? Cevabınız evet ise, bu e numarası biçimlendirmesinden nasıl kurtulacağınızı görmeye devam edin:

Örneğin: 23989488829399488881122334 gibi bir numaranız olabilir.

Şimdi bunu bir hücreye kopyalayın, ardından Excel otomatik olarak bilimsel biçimlendirmeyi kullanacaktır:

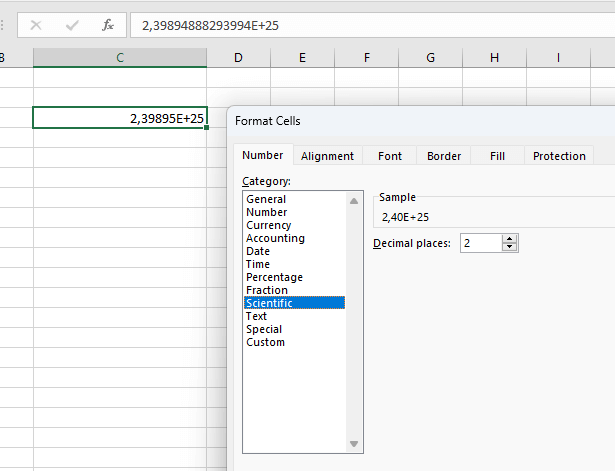
Şimdi, biçimlendirmeyi sıfır ondalıklı Sayı olarak değiştirmeniz yeterlidir:

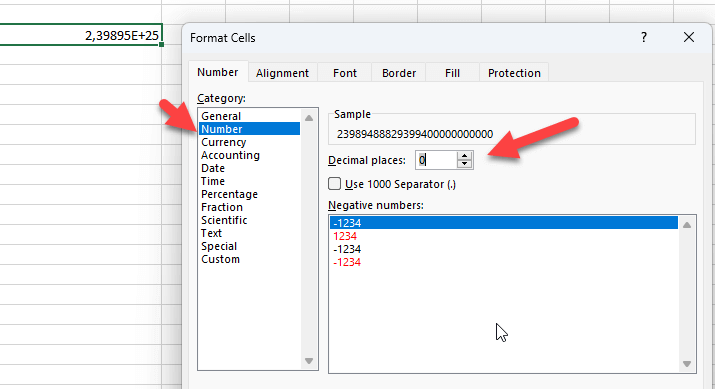
İyi görünüyor mu? Belki evet, ama aslında hayır. Bu yöntem size orijinal sayıdan farklı bir sayı verecektir:

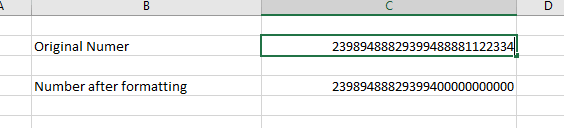
Oopps! Daha önce de belirttiğimiz gibi bu Excel’de bir biçimlendirme sorunu mu?

Bu sorundan nasıl kurtulurum?

Geçici bir çözüm var: Verilerinizi Excel’e aktarmadan önce başka bir elektronik tablo yazılımı kullanmalısınız. Ancak lütfen dosyanızı ilk etapta Excel’de açmamanız gerektiğini unutmayın. Orijinal dosya olarak kalmalıdır.

Umarım bu yardımcı olur!

Excel becerilerinizi geliştirmek istiyorsanız, Excel Formülleri Eğitmenimize göz atmayı unutmayın: Excel işlevlerini uygulamak için etkileşimli bir araç:

– Someka’nın Excel Formülleri Eğitim Aracı üç seviyede 30 farklı uygulama sunar –

8. Python’da Euler Sayısı Nasıl Kullanılır?

Python, çeşitli programlarda çalıştırılabilen ve dünya çapında yaygın olarak kullanılan bir programlama dilidir. Python, Euler’in sayısının önemi nedeniyle programlamada e’yi kullanmak ve hesaplamak için matematiksel komut sağlar.

Excel’de Euler Say ısına bir alternatif sağlamak için, Pyhton dilinde e sayısını kullanmayı da kısaca gözden geçireceğiz.

Python’da e değerine ulaşmanın iki yolu vardır. Bunlardan ilki“math.e” komutu, ikincisi ise yerleşik“exp ()” fonksiyonudur.

a) Python math.e komutu

Bu komut e veya pi gibi matematiksel değerleri içerir ve Python’da yaygın olarak kullanılır.

e değerini elde etmek için yapmanız gereken ilk şey matematik modüllerini içe aktarmaktır. Bunu yapmak için şunları yazmalısınız

“Matematiği içe aktar”

İlk satırda.

Yapılması gereken ikinci şey, e’nin değerini almak için kodu yazmaktır:

“print (math.e)”

ikinci satırda. “print” komutu programın kodunuzu çalıştırmasını sağlar.

Bunu çalıştırmak size yalnızca e değerini verecektir, ancak Python ile daha fazlasını hesaplayabilirsiniz.

Örneğin, eğer yazarsanız:

“print (math.e**2)”
Ya da
“print (pow(math.e, 2))”

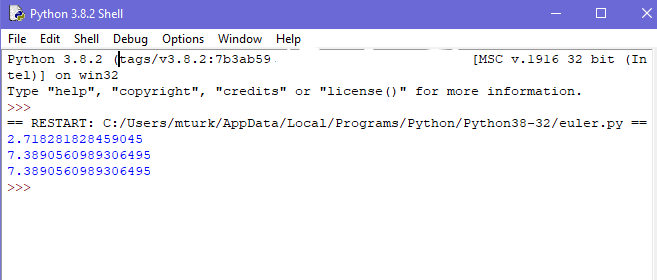
e2 değerine sahip olacaksınız. Bu komutların her ikisi de aynı şeyi hesaplar.

b) Python Yerleşik exp () fonksiyonu

Python belgelerine göre “math.e” sabitinden daha doğrudur.

Bunu kullanmak için yazarak başlamanız gerekir:

“Matematiği içe aktar”

İlk örnekte olduğu gibi. Tıpkı diğer örnekte olduğu gibi.

“exp ()” sözdizimi istediğiniz sayının kuvvetini verir. Örneğin, 3’ün kuvvetini istiyorsanız “exp (3)” yazmalısınız. Euler sayısının orijinal değerine sahip olmak için güç 1 olmalıdır. Bunu elde etmek için yazmalısınız:

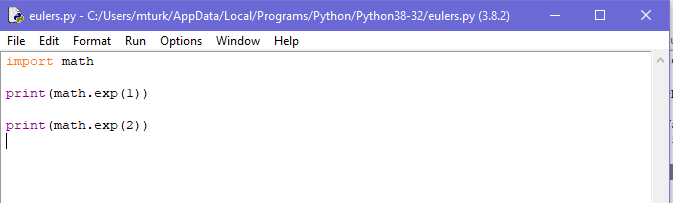
“print (math.exp(1)”

Bunu çalıştırmak size e değerini verecektir. e gücü gibi diğer değerleri hesaplamak istiyorsanız yazmanız gerekir:

“print (math.exp(2)”

Bunu çalıştırmak size e2 değerini verecektir.

Bu hesaplamaları çeşitlendirmek mümkündür. Python’da sadece e, sayı, boşluk, + ve – sembollerini içeren“evalExp()” adlı bir fonksiyon vardır. Bu, e ile basit bir hesaplama yapılmasını mümkün kılar.

Örneğin, 5e’ye 2 eklemek istiyorsanız tek yapmanız gereken yazmaktır:

“print (evalExp(‘5e+2’))”

Ve çalıştırdığınızda 15, 591409142295225 sonucunu alacaksınız.

9. Sonuç

Gördüğünüz gibi Euler sayısı hayatımız için çok önemlidir ve teknolojiden tıbba, fizikten finansa kadar birçok alanda kullanılmaktadır. Ayrıca matematikte, programlama dillerinde ve Excel’de kullanımı çok kolaydır. Kaçınmaya çalışmak daha fazla hesaplama yapmanıza neden olurken, ihtiyacınıza göre kullanmak hesaplamanızı basitleştirecektir. Excel’de Euler Sayısı makalemizi beğeneceğinizi umuyoruz.

Önerilen Okumalar:

Excel’de P Değeri: Nasıl Hesaplanır?

Excel’de Güven Aralığı Nasıl Hesaplanır?

Excel’de Verileri Nasıl Normalleştireceğinizi biliyor musunuz?