Fayda Matrisi (Payoff Matrix) Nedir? Önceliklendirme için Fayda Matrisleri Nasıl Kullanılır?

Bugün Fayda Matrisi kavramını keşfedeceğiz. Fayda matrisi nedir? Önceliklendirme ve iş kararları için nasıl kullanılır? Örnekler ve vaka çalışmaları ile faydalı rehber.

İçerik Tablosu

1. Fayda Matrisi nedir?
2. Fayda Matrisi ile İlgili Temel Kavramlar
3. Fayda Matrisi nasıl oluşturulur?
4. Tutsakların İkilemi
5. Fayda Matrisi Kullanarak Çözümler Nasıl Önceliklendirilir?
6. Fayda Matrisi Özeti
7. SSS

Fayda matrisi, ekonomi, iş stratejisi ve proje yönetimi gibi çeşitli sektörlerde uygulama alanı bulan oyun teorisinden ödünç alınmış bir kavram olan bu tür güçlü araçlardan biridir. Bu yazıda, ödül matrisinin ne olduğuna, ana unsurlarının neler olduğuna ve karmaşık ortamlarda çözümleri başarılı bir şekilde önceliklendirmek için nasıl kullanılabileceğine bakacağız.

1. Payoff Matrix nedir?

Getiri matrisi, oyun teorisi ve ekonomide oyuncular tarafından yapılan çeşitli stratejik eylemlerin potansiyel sonuçlarını göstermek ve analiz etmek için kullanılan bir araçtır.

Bu, her oyuncunun seçtiği stratejilere veya eylemlere bağlı olarak elde ettiği kazançları (yani kazançları veya kayıpları) gösteren bir tablodur. Matristeki her hücre, belirli bir strateji kombinasyonunun sonucunu yansıtmakta ve her oyuncunun kazancının tüm oyuncuların seçimlerinden nasıl etkilendiğini göstermektedir.

Matris, karar vericilerin birbirine bağımlı olduğu bir senaryonun en olası sonuçlarını tahmin etmeye yardımcı olur ve iş, siyaset veya sosyal ortamlardaki stratejik etkileşimleri değerlendirmek için yapılandırılmış bir yöntem sağlar.

2. Fayda Matrisine İlişkin Temel Kavramlar

Fayda matrisini anlamak için aşağıdaki temel kavramlara aşina olmak gerekir:

Oyuncular: Bunlar, stratejileri birbiriyle etkileşim halinde olan ve genellikle iki veya daha fazla olan senaryonun karar vericileridir.

Seçenekler: Her katılımcının seçebileceği bir dizi strateji veya eylem vardır.

Senaryo: Oyuncuların etkileşime girdiği ve kullanabilecekleri yöntemleri etkileyen belirli bir durum veya oyun.

Baskın Strateji: Rakibin planı ne olursa olsun, oyuncuyu daha iyi bir sonuca götüren bir strateji.

Nash Dengesi: Diğer oyuncular kendi stratejilerini korurken hiçbir oyuncunun kendi stratejisini değiştirmekten fayda sağlamadığı bir durumdur. Karşılıklı fayda sağlayan yanıtların olduğu bir durumu ifade eder.

Eyer Noktası: Sıfır toplamlı oyunlarda her iki oyuncunun stratejisinin de bir oyuncu için en düşük, diğeri için en yüksek kazançla sonuçlandığı durum.

Bu ilkeler, bir getiri matrisi içindeki dinamikleri incelemek ve anlamak için kritik öneme sahiptir ve oyuncuların çeşitli senaryolarda başarılı bir şekilde öngörüde bulunmasına ve strateji oluşturmasına olanak tanır.

3. Fayda Matrisi nasıl oluşturulur?

Bir fayda matrisi oluşturmanın çeşitli organize aşamaları vardır:

#Adım1: Oyuncuları Belirleyin:

Senaryonun oyuncularının kim olduğunu belirleyerek başlayın. Basit bir matrisin genellikle iki oyuncusu vardır.

#Adım2: Stratejilerin bir listesini yapın:

Her oyuncu için olası tüm stratejilerin veya eylemlerin bir listesini yapın. Bunlar kapsamlı ve birbirini dışlayıcı olmalıdır.

#Adım3: Matris Düzenini Oluşturun:

Bir oyuncunun stratejileri satırlarda, diğerinin stratejileri sütunlarda olacak şekilde bir tablo ya da ızgara oluşturun.

#Adım4: Getirilerinizi belirleyin:

Seçilen stratejilerin karışımı göz önüne alındığında, matrisin her bir hücresinde her iki oyuncu için sonucu veya ödülü belirleyin. Bu getirileri hesaplamak için kâr, maliyet, fayda veya diğer uygulanabilir ölçütler kullanılabilir.

#Adım5: Matristeki boşlukları doldurun:

Matrisi tamamlamak için her strateji kombinasyonu için getirileri doldurun. Her hücre her iki oyuncu için de sonucu göstermelidir.

#Adım6: Denge için inceleyin:

Matris tamamlandığında, Nash Dengeleri veya baskın stratejiler için inceleyin.

Bir getiri matrisinin oluşturulması, matrisin tartışılan stratejik senaryoyu uygun şekilde yansıtmasını sağlamak için tüm potansiyel etkileşimlerin ve sonuçların kapsamlı bir şekilde incelenmesini gerektirir.

4. Mahkumların İkilemi

Tutsakların İkilemi, kazanç matrislerinin nasıl çalıştığını gösteren klasik bir oyun teorisi örneğidir. Bu senaryoda iki dolandırıcı yakalanır ve ayrı ayrı sorgulanır. Sevgililerine ihanet edip aleyhlerinde tanıklık etmek ile sessiz kalmak arasında seçim yapmak zorundadırlar. Bu senaryonun kazanç matrisi dört olası sonuç sunmaktadır.

• Eğer her iki mahkum da birbirlerine ihanet ederse, her biri orta derecede ceza alacaktır.
• Her ikisi de sessiz kalırsa, kanıt yetersizliği nedeniyle hafif bir ceza alacaklardır.
• Biri İhanet Eder, Biri Sessiz Kalır: Eğer biri ihanet eder ve diğeri sessiz kalırsa, ihanet eden serbest kalırken, sessiz kalan hapse mahkum edilir.

Optimum kolektif sonuç her ikisinin de sessiz kalması olsa da, her mahkumun ihanet etmek için güçlü bir bireysel teşviki vardır, bu da her ikisi için de daha az ideal bir sonuçla sonuçlanır.

5. Fayda Matrisi Kullanarak Çözümler Nasıl Önceliklendirilir?

Bir getiri matrisi, çeşitli karar verme durumlarında çözümlere öncelik vermek için yararlı bir araç olabilir.

Öncelikle önceliklendirme ve iş kararları için ödül matrislerini nasıl kullanabileceğinize dair adımlarımızı sıralayalım:

1. Karar Bağlamını Oluşturun: Çözümlerin önceliklendirildiği durumu veya sorunu ayrıntılı olarak ana hatlarıyla belirtin.
2. Potansiyel Çözümleri Belirleyin: Tüm olası seçeneklerin bir listesini yapın. Bunlar matrisinizin bir boyutunu oluşturacaktır (satırlar veya sütunlar).
3. Değerlendirme Kriterlerini Oluşturun: Her bir çözümü değerlendirmek için kullanacağınız kriterleri belirleyin. Bu kriterler matrisinizin ikinci boyutunu oluşturacaktır.
4. Fayda değeri atanmalıdır: Bir çözüm ile matrisinizdeki bir kriterin her kesişimine bir fayda değeri atayın. Bu değer, verilen kriterle ilgili olarak çözümün etkinliğini veya faydasını göstermelidir.

1. Matrisi İnceleyin: Kriterlerinize göre hangi çözümlerin en iyi toplam getiriye sahip olduğunu belirlemek için tamamlanmış matrisi inceleyin.
2. Farklı Bakış Açılarını Dikkate Alın: Mümkünse, ödül değerlerini değiştirebilecek çeşitli paydaş bakış açılarını matrise dahil edin.
3. Bilgilendirilmiş Seçimler Yapın: En büyük genel avantajları sağlayan çözümleri seçmek için matrisin bulgularını kullanın.

Bu bağlamda, getiri matrisi, tüm olasılıkların kritik kriterlere göre dikkatlice değerlendirilmesini sağlayarak karar verme sürecinde organize ve karşılaştırmalı bir yaklaşımı teşvik eder.

Örnek Çalışma 1 – Fayda matrisi ile önceliklendirme

Bu vaka çalışması, pazarlama kararını vermeye çalışan bir şirket örneği verecektir.

Senaryo: Pazarlama Stratejisi Kararı

Küçük bir teknoloji girişimi olan ABC, önümüzdeki çeyrek için pazarlama stratejisine karar veriyor. Şirket iki seçenek arasında kalmıştır: dijital bir pazarlama kampanyası (Seçenek A) ve basılı ve medya reklamlarını içeren geleneksel bir pazarlama yaklaşımı (Seçenek B). Her bir stratejinin etkinliği pazarın vereceği tepkiye bağlıdır; bu tepki yüksek düzeyde alıcı (Senaryo 1) ya da orta düzeyde alıcı (Senaryo 2) olabilir.

Seçenekler:

• Seçenek A: Dijital Pazarlama Kampanyası
• Seçenek B: Geleneksel Pazarlama Kampanyası

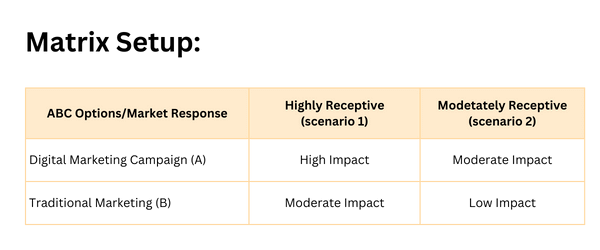
Matris Kurulumu:

Fayda matrisimizi kurmayacağız:

Matris Kazançları:

• Yüksek Etki: Müşteri bağlılığında ve satışlarda önemli artış.
• Orta Düzey Etki: Gözle görülür iyileşme ancak ‘Yüksek Etki’ kadar önemli değil.
• Düşük Etki: Katılım ve satışlarda minimum iyileşme.

Sonuçlar:

Pazarın yüksek düzeyde alıcı olması durumunda (Senaryo 1), Dijital Pazarlama Kampanyası (Seçenek A) Yüksek Etki yaratırken, Geleneksel Pazarlama Kampanyası (Seçenek B) yalnızca Orta Düzeyde Etki yaratacaktır. Eğer piyasa orta düzeyde alıcı ise (Senaryo 2), A Seçeneği yine Orta Düzeyde Etkiye yol açarken, B Seçeneği Düşük Düzeyde Etki ile sonuçlanır.

Getiri matrisine göre, Dijital Pazarlama Kampanyası (Seçenek A) her iki senaryoda da en azından orta düzeyde başarı sağladığı için daha sağlam bir stratejidir. Buna karşılık, Geleneksel Pazarlama Kampanyası (Seçenek B), pazarın yalnızca orta düzeyde alıcı olması halinde düşük bir etkiye sahip olma riski taşımaktadır. Bu nedenle TechNovate, önümüzdeki çeyrek stratejisi için Dijital Pazarlama Kampanyasına öncelik vermeyi düşünmelidir.

Vaka Çalışması 2 – Fayda matrisi ile iş rekabeti

Bu vaka çalışması, iki sanat koleksiyoncusu arasındaki bir vaka çalışmasını inceleyecektir.

Senaryo Açık Artırma Teklifi

Bu senaryoda, iki rakip sanat koleksiyoncusu, Alice ve Bob, bir açık artırmada nadir bir tablo için teklif vermektedir. Her birinin iki seçeneği vardır: yüksek teklif vermek (Seçenek H) veya düşük teklif vermek (Seçenek L). Teklif için mevcut olan toplam para miktarı sabittir ve sonuç onların bireysel teklif stratejilerine bağlıdır. Daha yüksek teklif veren tabloyu kazanır, ancak daha yüksek bir maliyetle, daha düşük teklif veren ise paradan tasarruf eder ancak tabloyu kaybetme riskiyle karşı karşıya kalır.

Oyuncular:

1. Alice
2. Bob

Her Oyuncu için Seçenekler:

• Seçenek H: Yüksek Teklif Verin
• Seçenek L: Düşük Teklif

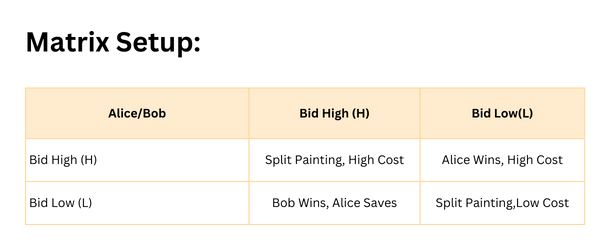
Matris Kurulumu:

Fayda matrisimizi şu şekilde oluşturabiliriz:

Matris Kazançları:

• Bölünmüş Boyama, Yüksek Maliyet: Her iki oyuncu da yüksek teklif verir ve toplam bölünür; her ikisi de yüksek maliyete katlanır.
• Alice Kazanır, Yüksek Maliyet: Alice yüksek teklif verir ve kazanır, ancak daha yüksek bir maliyetle, Bob ise parasını kurtarır.
• Bob Kazanır, Alice Tasarruf Eder: Bob yüksek teklif verir ve kazanır, Alice düşük teklif vererek tasarruf eder.
• Bölünmüş Boyama, Düşük Maliyet: Her ikisi de düşük teklif verir, ikisi de boyamayı kazanamaz, ancak her ikisi de paradan tasarruf eder.

Sonuçlar:

• Hem Alice hem de Bob Yüksek (H) Teklif verirse, tabloyu paylaşırlar ancak yüksek maliyetlere katlanırlar.
• Alice Yüksek (H) ve Bob Düşük (L) Teklif verirse, Alice tabloyu yüksek bir maliyetle kazanır.
• Tersine, Alice Düşük (L) ve Bob Yüksek (H) Teklif verirse, Bob tabloyu kazanır ve Alice parasını kurtarır.
• Her ikisi de Düşük Teklif (L) verirse, ikisi de tabloyu kazanamaz, ancak her ikisi de paradan tasarruf eder, sonuçta her biri için düşük bir maliyetle toplamın bölünmesi sağlanır.

Bu kazanç matrisi, toplam miktarın sabit kaldığı ve oyuncuların seçimlerinin bireysel kazançlarını veya kayıplarını doğrudan etkilediği klasik bir sabit toplamlı oyunu göstermektedir.

Önceliklendirme ve Karar Verme Araçları

İş kararlarınızı kolaylaştırmak için önceliklendirme veya strateji oluşturma araçlarını kullanabilirsiniz. Operasyonel süreçlerinize yardımcı olması için iş stratejisi şablonlarını deneyebilirsiniz.

Günlük görevlerinizi önceliklendirmek için kullanımı kolay bir çözüm arıyorsanız, önceliklendirme araçlarımızı deneyin:

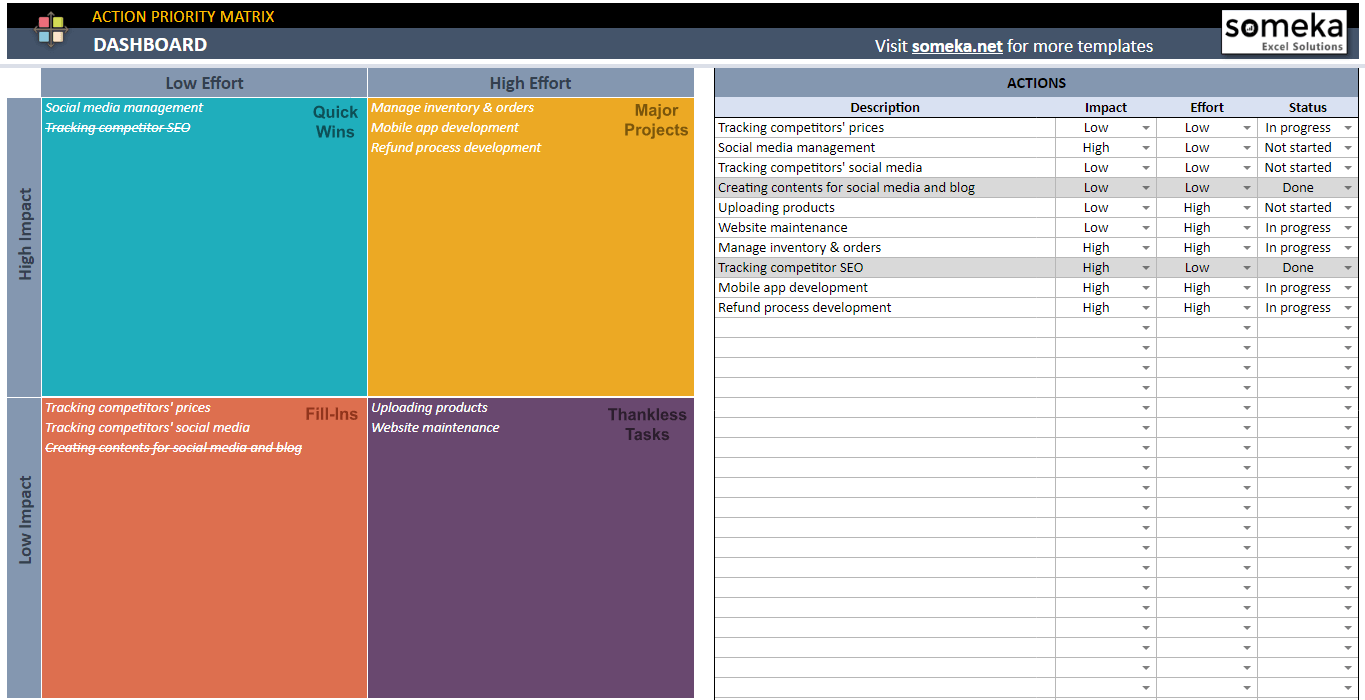
– Bu görsel Someka tarafından hazırlanan Eylem Öncelik Matrisi Google E-Tablolar Şablonundan alınmıştır –

Bir başka araç da karar matrisimiz olabilir:

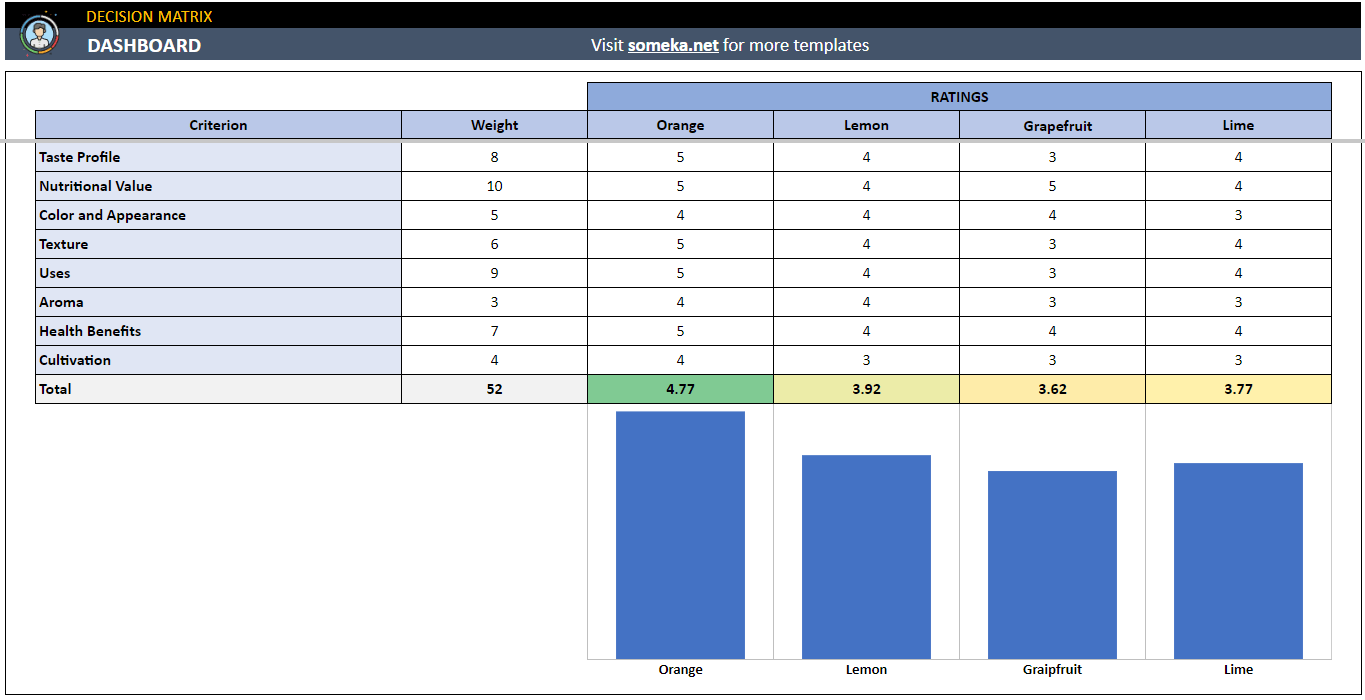
– Bu görsel Someka tarafından hazırlanan Karar Matrisi Google E-Tablolar Şablonundan alınmıştır –

6. Fayda Matrisi Özeti

Son olarak, getiri matrisi stratejik karar verme cephaneliğinde çok çeşitli ve güçlü bir araçtır. Uygulamaları, Tutsakların İkilemi gibi karmaşık oyun teorisi problemlerini basitleştirmekten günlük iş seçimlerine yardımcı olmaya ve çeşitli disiplinlerde çözümleri önceliklendirmeye kadar uzanmaktadır.

Bir getiri matrisinin etkinliği, çeşitli taktiklerin veya eylemlerin sonuçlarını görsel olarak tanımlama ve karşılaştırma kapasitesinde yatar ve karmaşık durumları daha anlaşılır ve kontrol edilebilir hale getirir.

7. SSS

Fayda matrisleri ile ilgili en yaygın soruları yanıtlamaya çalışacağız.

Oyun teorisinde getiri nedir?

Bir kazanç, bir oyuncunun bir oyunda belirli bir eylem veya stratejiden elde ettiği sonuç veya ödüldür. Sıklıkla fayda, kar veya diğer ilgili ölçütler açısından ölçülen bu sonuç, tüm oyun oyuncuları tarafından seçilen stratejiler kümesi tarafından belirlenir.

Kazançlar oyun teorisinin önemli bir parçasıdır çünkü oyuncuların kararlarının sonuçlarını anlamalarına yardımcı olur ve bu kararları verirken onlara yol gösterir. Stratejik oyunlardaki oyuncular, kendilerinin ve diğerlerinin kullandığı stratejilere dayalı olarak kazançlarını en üst düzeye çıkarmaya çalışırlar.

Bir piyasa yapısının getiri matrisi nedir?

Bir piyasa yapısının getiri matrisi, belirli bir piyasadaki işletmeler tarafından yapılan çeşitli stratejik eylemlerin sonuçlarını incelemek için kullanılan ekonomik bir araçtır. Her bir firma için getirilerin (kar veya pazar payı gibi) pazardaki tüm işletmeler tarafından alınan stratejik kararlar tarafından nasıl belirlendiğini gösterir.

Örneğin bir oligopol piyasasında matris, rakip firmalar tarafından kullanılan farklı fiyatlandırma taktiklerinin göreceli getirilerini nasıl etkilediğini gösterebilir. Bu matris, işletmelere rekabetçi etkileşimlerin potansiyel sonuçlarını öngörme ve buna göre strateji belirleme konusunda yardımcı olur.

Önerilen Okumalar:

Daha İyi Kararlar Almak İçin Excel’de Karar Matrisi Nasıl Yapılır?

Altı Sigma Metodolojisi: Tanım ve Hakkında Tam Genel Bakış

Doğrusal Programlama için Excel Çözücü nasıl kullanılır: Optimizasyon Problemlerinin Çözümü