P Değeri Nedir? Excel’de P Değeri Nasıl Hesaplanır?
İçindekiler
P Değeri Nedir?
P-değeri, kullandığınız hipotezin doğru olması durumunda örnekleme varyasyonunun olasılığını belirlemenize yardımcı olan bir istatistik terimidir. Basitçe, sıfır hipotezimiz doğruysa bu sonuçları elde etme olasılığımızın ne olduğunu söyler.
-
- Bir null hipotezi, elde ettiğimiz sonuçların tamamen şanstan kaynaklandığını iddia eden bir hipotezdir
.
- Bir alternatif hipotez, elde ettiğimiz sonuçların şans olmadığını, sonuçlarımızı etkileyen dış unsurlar olduğunu iddia eder.
Çok önemli ve yaygın olarak kullanılan bir istatistik terimidir ve Microsoft Excel gibi veri analiz programlarında kolayca hesaplanabilir. Bu makalede, nasıl kullandığımızı, nerelerde kullandığımızı ve Excel’de çeşitli şekillerde nasıl hesaplayabileceğimizi öğreneceksiniz.
Hadi başlayalım!
Neden P-Değerine İhtiyacımız Var?
Büyük popülasyonlarla araştırma yaparken her bir birey için istatistikleri hesaplamanız gerekir. Ancak böyle bir durumda bile, her şeyi gözlemlemek imkansız olduğu için bir şeyin tesadüf mü yoksa şans eseri mi olduğundan emin olamazsınız. İşte istatistik burada devreye girer.
İstatistiksel hesaplamalar size mutlak gerçeği veremez, ancak araştırmalarınız hakkında iyi bir fikir sahibi olmanıza yardımcı olur.
P-değeri, konumuzla ilgili hipotezleri test etmemizi sağlar. Matematiksel sonuçları bu hipotezlerle karşılaştırabilir ve araştırma için çok fazla zaman harcamadan yolumuzu yeniden gözden geçirebiliriz.
P Değerini Gerçek Hayatta Nerede Kullanırız?
Olasılık değerini bir hipotezi test etmeye çalıştığımız durumlarda kullanırız. Bu bir araştırma ya da arkadaşımızla girdiğimiz basit bir bahisle ilgili olabilir.
Bunu örneklerle anlamak daha kolay.
Pazarlama:
Diyelim ki pazarlama alanında çalışıyorsunuz ve son projeniz tahıl reklamcılığı üzerine.
Sosyal medya için bir video hazırladınız ve kullanıcıların atladığı ya da uzun süre izlediği bilgisine sahipsiniz.
Örnek olarak, videonun ortak izlenme süresi 20 saniyedir. Ortalama ise 20 saniyedir. Ve videoyu daha neşeli bir müzik parçasıyla düzenleme kararı aldınız.
Şimdi işe yarayıp yaramadığını nasıl anlayacaksınız? Bu noktada önemlilik istatistiklerini kullanıyoruz.
İlk olarak, bir sıfır hipotezi üretin:
Sıfır hipotezi, yaptığınız yatırım ile elde ettiğiniz sonuçlar arasında hiçbir korelasyon olmadığını iddia eder. Sonuçları etkilemez.
Bu örnek sırasında boş hipotez şu olacaktır: “Saat zamanına uyguladığınız değişiklikler arasında herhangi bir ilişki yoktur.”
O halde, alternatif hipotez:
Alternatif hipotez, aslında müziği değiştirmenin işe yaradığını ve artık insanların reklamı 20 saniyeden fazla izlediğini öne sürüyor. Matematiksel olarak alternatif hipotez şöyle der:
“Ortalama şu anda 20 saniyeden fazla.”
Önemlilik Düzeyini Hesaplayın:
Şimdi başarılı olup olmadığımızı hesaplamak için bir sınır eşiği belirlemeliyiz. Buna anlamlılık düzeyi denir ve ayrıca alfa değeri olarak da anılır. İstediğiniz herhangi bir yüzde olabilir, bu kesinlikle size kalmış.
Ancak bu örnek sırasında 0,05 olacaktır.
Şimdi kesin olarak hesaplamak için her zaman saat zamanının tüm verilerine sahip olmalıyız. Ancak zaman ve kaynaklarınız açısından, popülasyondan bir örneklem almalısınız:
- 100 kişilik bir örneklem aldınız.
- Bu 100 kişinin reklam için 25 saniye izleme süresi vardır.
- Örneklem ortalamasının 25 olduğu anlamına gelir.
Bu, hesaplamanın çok basit bir versiyonudur. Ancak, tüm popülasyonun standart sapmasını bilmiyorsanız, örneklemin standart sapması genellikle bu ölçekte hesaplanır.
Popülasyon değerlerine yakın oldukları için örneklem için hesapladığınız değerleri kullanabilirsiniz. Örneklem ortalaması popülasyon ortalamasına yakındır.
P-Değerini Hesaplayın:
p-değeri bize sıfır hipotezini reddedip reddedemeyeceğimizi gösterir. sıfır hipotezi doğru kabul edildiğinde örnek ortalamasının 25 dakikadan büyük veya eşit olma olasılığı.
Olabilecek iki durum vardır.
- Eğer p-değeri alfadan küçükse, sıfır hipotezini reddedebilirsiniz . Alternatif hipotezin doğru olduğuna dair istatistiksel kanıt elde etmiş olursunuz.
- Ancak p-değeri alfa değerinden büyük veya eşitse, sıfır hipotezini reddedemezsiniz. Bu, sıfır hipotezinin kesinlikle doğru olduğu anlamına gelmez, ancak bundan da kaçınılamaz.
Olasılık
Başka bir örnek üzerinde çalışalım.
Arkadaşınız ve siz havaya yazı tura attınız: Eğer kuyruk gelirse 5 dolar kaybedersiniz, tura gelirse 5 dolar kazanırsınız.
- Arkadaşınız yazı turayı bir kez atıyor: Yazı geliyor. Sorun değil, yazı gelmesi için %50 şans var. Şimdi, adil bir para olduğuna inandığınız için olasılığın 0,5 olduğunu varsayıyorsunuz. Bu sizin sıfır hipotezinizdir.
- İkincisi: Yazı. 5 dolar daha kaybettiniz ama sorun değil çünkü arka arkaya iki yazı gelme ihtimali hala yüksek. P-değeri 0,25 ve bu hala adil bir oran.
- Üçüncüsü: bir kez daha yazıdır. Arka arkaya üç kez yazı gelme olasılığı 0,12’dir. Bu düşük değildir, bu nedenle sıfır hipotezinin doğru olmadığına dair yeterli kanıt yoktur. Ancak alternatif hipotezinizin doğru olabileceğini düşünmeye başlarsınız.
- Dördüncü: Yine yazı gelirse şansın ne kadar azaldığını göreceksiniz. Mucizevi bir tesadüf olabilir ama hala 0,6 şans var ve hala madalyonun hileli olduğunu söyleyen alternatif hipotezi desteklemek için yeterli kanıt yok. Ve beşinci yazı turayı beklersiniz.
- Beşinci: Bu yazıdır. Bir madeni paranın arka arkaya beş kez yazı gelme olasılığı 0,3’tür ve bu çok düşüktür. Bu, artık onu destekleyecek yeterli kanıt olmadığı için sıfır hipotezini reddedebileceğiniz noktadır.
Arkadaşınızdan parayı görmesini istiyorsunuz ve parayı elinize aldığınızda iki yazı tarafı olduğunu ve hileli bir para olduğunu fark ediyorsunuz.
Sıfır hipotezimize olan inancımızı kaybetmemize ne sebep oldu?
Adil bir yazı tura oyununda yazı veya tura gelme ihtimali %50’dir. Bu, paranın adil olduğuna inandığımız bir durumdur, ancak p-değeri düştükçe bu hipoteze olan güvenimiz de zayıflar.
P-değeri 0,05’in altına düştüğünde rastgele kuyrukların olma ihtimali çok azdır. Dolayısıyla bu istatistiksel terimi kanser araştırmaları veya iklim değişikliğinin etkileri gibi konulara uyguladığınızda daha fazla önem kazanır.
Not: Varsayılan hesaplama için 0,05 p-değeri kullanmamızın özel bir nedeni yoktur. Formülün yaratıcısı bunun hesaplama için iyi bir sayı olduğuna karar verdi ve varsayılan hesaplamalar buna bağlı kaldı.
0,05 100 bireylik popülasyonda %5 anlamına gelir ki bu da normal eğriye girer. Yaygın olarak kullanılmasının nedenlerinden biri de budur. Kendiniz hesaplarken değiştirmek isterseniz, değiştirebilirsiniz.
Excel’de P-Değeri Nasıl Hesaplanır?
Microsoft Excel’de p-değerini hesaplamanın birden fazla yolu vardır. Formülleri yazabilir veya Analiz ToolPak‘ı kullanabilirsiniz. Bu makale her iki yöntemin de nasıl yapılacağını içermektedir.
Klasik Excel Formüllerinin Kullanımı:
Klasik Excel formülü yolu ile başlayalım. Bunu yapmanın iki yolu vardır TDIST formülü ve T-test formülü.
1.1) TDIST Formülü
Öncelikle, p-değerini hesaplamak için bir veri setine ihtiyacınız olacaktır.
-
- Diyelim ki öğretmensiniz ve öğrencilerinizin son sınavda aldığı puan ile önceki sınavlarına göre puanlarının ne olmasını beklediğinizi karşılaştırmak istiyorsunuz.
- Son sınavınız için 25, 46, 34, 27, 35, 43, 40, 44, 21 ve 39 numaralı sonuçlara sahipsiniz
.
- Şimdi hesaplama için başka bir kuyruğa ihtiyacınız var, bu önceki testlere göre beklediğiniz puan: 23, 44, 32, 20, 46, 37, 35, 42, 33 ve 35
Şimdi, Excel’de p-değeri formülünü kullanmak için önceden birkaç şeyi hesaplamanız gerekir:
Pearson katsayısı (r): İki veri arasındaki doğrusal korelasyonu ölçen istatistiksel bir terimdir. P-değerini hesaplamak için matematiksel yönünü bilmek zorunda değilsiniz. İlerleyen paragraflarda bunun basit formülünü göreceksiniz.
Popülasyon (n): n, veri setinizdeki toplam birey sayısıdır.
T istatistiği: Verinin tahmin edilen değerinin varsayılan değerinden sapmasının standart hatasına oranıdır.
Serbestlik derecesi: Veri setindeki birey sayısı eksi ikidir.
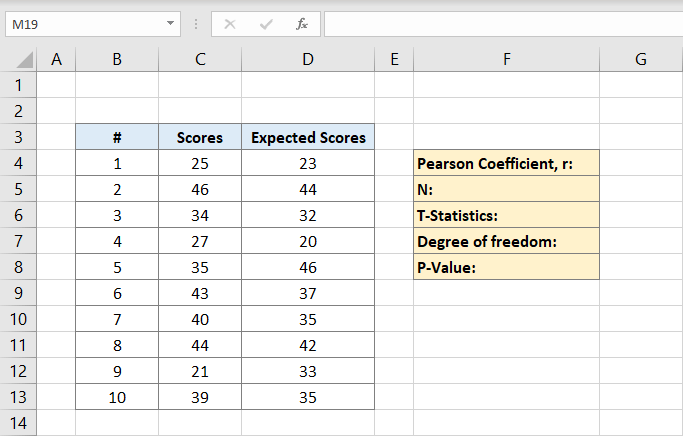
Şimdi, Pearson katsayısı bu örnekte F4’e yazılacaktır. Ona tıkladıktan sonra formülü yazacaksınız:
C sütunları puanlar için, D sütunları ise beklenen puanlar içindir. Bu örnekte Pearson katsayısı 0,691473’tür.
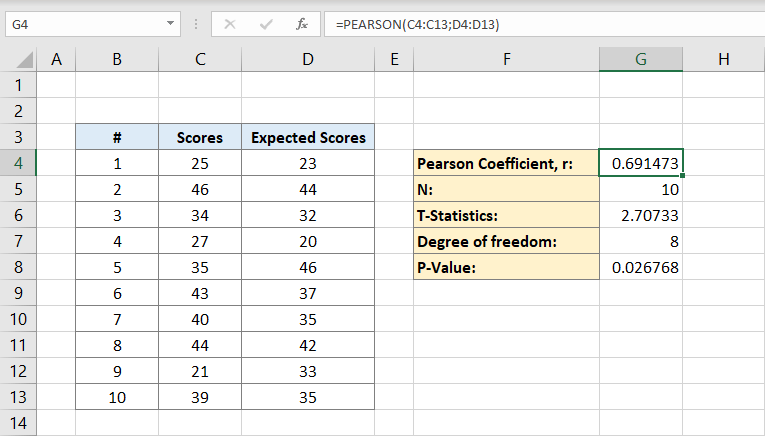
Ardından, veri setindeki birey sayısını yazacaksınız. Kaç bireye sahip olduğunuzu kesinlikle biliyorsanız, bunu manuel olarak yazabilirsiniz, ancak bilmiyorsanız formülü kullanabilirsiniz:
Formül neden yalnızca C sütununu içeriyor?
Bunun nedeni, hesaplama yapmak için yalnızca bir veri setindeki bireylere ihtiyacımız olmasıdır, bu nedenle tek bir sütun yeterli olacaktır. G5 hücresi şimdi içinde 10 sayısını içerecektir. Bu bizim nüfusumuzdur.
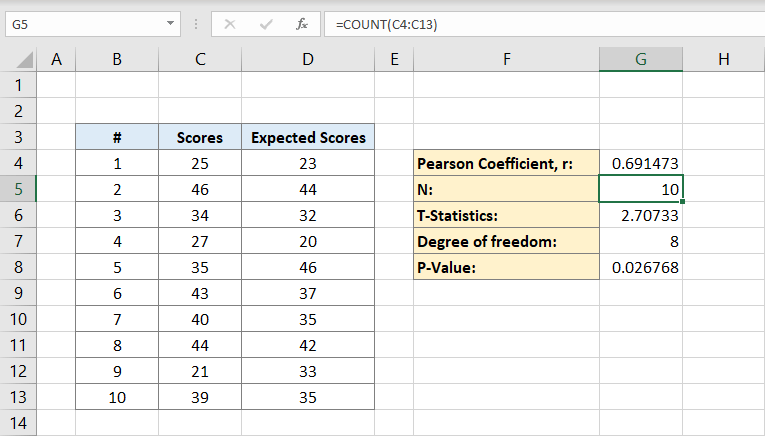
Artık hem Pearson katsayısına hem de nüfusa sahip olduğunuza göre T istatistiklerini hesaplayabilirsiniz. T istatistiğinin matematiksel formülü Pearson katsayısı (r) çarpı işaret karekökü nüfus (n) eksi 2 bölü 1 eksi Pearson katsayısının kareköküdür:
G6 hücresi 2,70733 sonucunu içerecektir. Bu bizim T istatistiğimizdir.
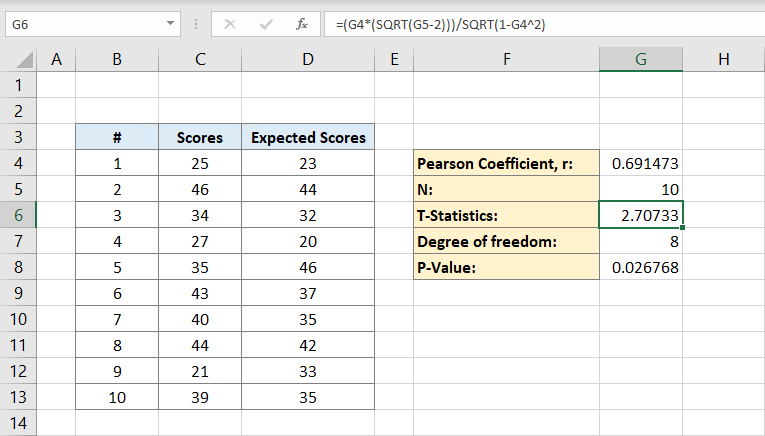
Bundan sonra, serbestlik derecesini hesaplayacaksınız. Yazacaksınız:
G7 hücresine. Bu serbestlik derecesidir. 8’de olacak.
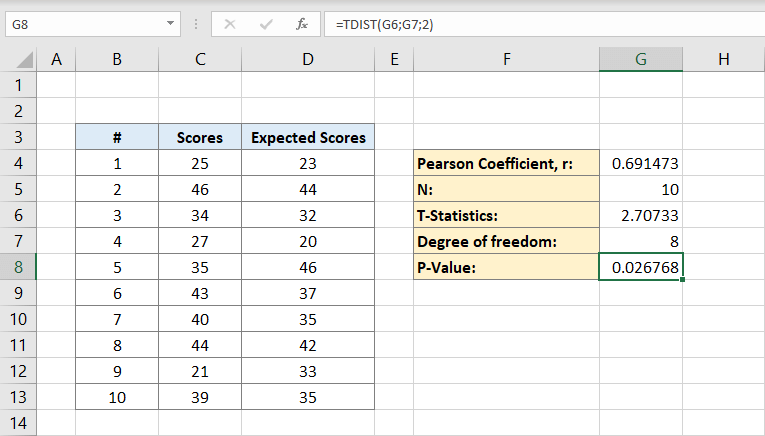
Artık P-değerini hesaplamak için ihtiyacınız olan her şeye sahipsiniz. G8 hücresi bunun formülünü içerecektir. Yani:
Ya da
Sonuç 0,026768 olacaktır. Bu, veri seti için p-değeridir.
1.2. T-Testi Formülü
Excel formülleri ile p-değerini belirlemenin ikinci yolu T-test formülünü kullanmaktır. Bir önceki örneğe biraz benzer ancak daha kısadır.
-
- Veri setinin aynı olduğunu varsayalım, son sınavınız için 25, 46, 34, 27, 35,43, 40, 44, 21, 39 sonuçlarına sahipsiniz
.
- Beklenen sonuçlar 23, 44, 32, 20, 46, 37, 35, 42, 33, 35.
- Beklenen puan ile gerçek puan arasındaki fark için üçüncü bir sütun ekleyeceksiniz. Fark sütununa E4’ten E13’e kadar 2, 2, 2, 7, 11, 6, 5, 2, 12, 4 yazılacaktır.
Şimdi E8 hücresine T-Testi yazın. T-testi formülünü yanındaki boş hücreye yazacaksınız. Yani:
Ve bu formül size doğrudan p-değerini verecektir.
Excel Araç Paketi ile P-Değerini Belirleyin
Took Pak, çeşitli istatistiksel ölçümleri otomatik olarak hesaplamanıza olanak tanıyan bir pakettir, bu nedenle kolay ve çok kullanışlıdır. Kurulumu da kolaydır.
Adım 1: Ayarlara gidin. Sol köşenin altında bir “Eklentiler” düğmesi var, ona tıklayın. Yeni bir pencere açılacak, “Analysis Tool Pak” seçeneğini bulun, tıklayın ve ardından pencerenin altındaki git düğmesine tıklayın.
Adım 2: Sağ sütundaki Tamam düğmesinden sonra yanındaki tik işaretine tıklayarak eklentiyi etkinleştirin.
Adım 3: Doğru şekilde etkinleştirmeyi başardıysanız, çalışma sayfanızın üst menüsünde sağ tarafta bir “Veri analizi” düğmesi görünecektir.
Adım 4: “Veri analizi” düğmesine tıklayın ve “t-Testi: Paired Two Sample for Means” seçeneğini seçin. Bundan sonra Tamam’a tıklayın. Yeni bir pencere açılacaktır.
Adım 5: Pencerenin ilk satırındaki girdileri soracaktır. “Değişken 1 aralığı” kutusuna C4: C13 yazacaksınız. “Değişken 2 aralığı” kutusuna D4: D13 yazacaksınız. Alfa kutusunu varsayılan değeri ile bırakın.
Adım 6: Pencerenin ikinci satırında sonuçlarınızı nerede izleyeceğinizi seçebilirsiniz. Yeni bir çalışma sayfası veya herhangi bir boş hücre olabilir. Eğer sonucu bir hücrede görmek istiyorsanız sütunu ve satırı kilitlediğinizden emin olun. Bundan sonra Tamam düğmesine tıklayın.
İpucu: Sütun ve satırı kilitlemek için harf ve sayıdan önce dolar işaretini kullanın. Örneğin, A2 hücresini kilitlemek istiyorsanız $A$2.
yazın.
Adım 7: Excel ortalamayı, varyansı, gözlemleri, Pearson korelasyonunu, varsayılan ortalama farkı, t istatistiklerini, p değerini ve daha fazlasını hesaplayacaktır.
SON SÖZLER
P-değerinin hesaplanması ve birçok farklı duruma uyarlanması kolaydır. Çok fazla zaman veya çaba harcamadan ihtiyacınız olan bilgileri elde etmenize yardımcı olur. Doğru araçlar ve formüllerle birlikte gelen Microsoft Excel gibi istatistiksel analiz programlarını kullandığınızda hesaplanması daha da kolaydır. Someka şablonları koleksiyonuna göz atalım ve işinizi kolaylaştırmak için istatistiksel şablonları indirelim!


