What’s Payoff Matrix? How to use Payoff Matrices for Prioritization?

Today we’re going to discover the Payoff Matrix concept. What’s a payoff matrix? How to use it for prioritization and for business decisions? With examples and case studies.

Table Of Content

1. What is Payoff Matrix?
2. Key Concepts on Payoff Matrix
3. How to create a Payoff Matrix?
4. The Prisoners’ Dilemma
5. How to Prioritize Solutions Using a Payoff Matrix?
6. Payoff Matrix Wrap up
7. FAQ’s

The payoff matrix is one such strong tool, a notion borrowed from game theory that has found applications in a variety of sectors such as economics, business strategy, and project management. In this post, we will look at what a reward matrix is, what its major elements are, and how it may be used to successfully prioritize solutions in complex settings.

1. What is Payoff Matrix?

A payoff matrix is a tool used in game theory and economics to display and analyze the potential outcomes of various strategic actions made by players.

It’s a table that shows the payoffs (i.e., gains or losses) for each player based on the strategies or actions they choose. Each cell in the matrix reflects the outcome of a certain strategy combination, demonstrating how the payoff for each player is influenced by the choices of all players.

The matrix aids in forecasting the most likely outcomes of a scenario in which decision-makers are interdependent, and it provides a structured method for evaluating strategic interactions in business, politics, or social settings.

2. Key Concepts on Payoff Matrix

Understanding the payout matrix necessitates familiarity with the following fundamental concepts:

Players: These are the scenario’s decision-makers, usually two or more, whose strategies interact with one another.

Options: Each participant has a set of strategies or actions from which to pick.

Scenario: A specific situation or game in which the players interact, impacting the methods they may employ.

Dominant Strategy: A strategy that, regardless of the opponent’s plan, leads in a better end for the player.

Nash Equilibrium: A condition in which no player benefits from changing their strategy while the other players maintain theirs. It denotes a state of mutually beneficial replies.

Saddle Point: A condition in zero-sum games in which both players’ strategies result in the lowest payout for one player and the highest payoff for the other.

These principles are critical in studying and comprehending the dynamics inside a payout matrix, allowing players to successfully anticipate and strategize in diverse scenarios.

3. How to create a Payoff Matrix?

There are various organized phases involved in creating a pay-off matrix:

#Step1: Determine the Players:

Begin by determining who the scenario’s players are. A simple matrix often has two players.

#Step2: Make a list of the strategies:

Make a list of all possible strategies or actions for each player. These must be exhaustive and mutually exclusive.

#Step3: Create the Matrix Layout:

Make a grid or table with one player’s strategies down the rows and the other’s down the columns.

#Step4: Determine your payoffs:

Determine the outcome or reward for both players in each cell of the matrix, given the mix of strategies chosen. Profit, cost, utility, or any other applicable measure can be used to calculate these payoffs.

#Step5: Fill in the blanks in the matrix:

Fill in the payoffs for each strategy combination to complete the matrix. Each cell should display the result for both players.

#Step6: Examine for equilibrium:

When the matrix is complete, examine it for Nash Equilibria or dominating strategies.

Creating a payoff matrix necessitates thorough study of all potential interactions and outcomes, ensuring that the matrix appropriately reflects the strategic scenario under discussion.

4. The Prisoners’ Dilemma

The Prisoners’ Dilemma is a classic game theory example that demonstrates how payoff matrices work. Two crooks are captured and interrogated individually in this scenario. They must choose between betraying their lover and testifying against them and remaining silent. This scenario’s payoff matrix offers four possible outcomes.

• If both inmates betray each other, they will each receive a moderate punishment.
• If both keep silent, they will receive a light punishment due to a lack of evidence.
• One Betrays, One Remains mute: If one betrays and the other remains mute, the betrayer is free, while the silent one is sentenced to prison.

While the optimum collective outcome is for both to remain silent, each prisoner has a strong individual incentive to betray, resulting in a less ideal outcome for both.

5. How to Prioritize Solutions Using a Payoff Matrix?

A payoff matrix can be a useful tool for prioritizing solutions in a variety of decision-making situations.

First list our steps about how you can use reward matrices for prioritization and business decisions:

1. Establish the Decision Context: Outline the situation or problem for which solutions are being prioritized in detail.
2. Determine Potential Solutions: Make a list of all possible options. These will constitute one dimension of your matrix (rows or columns).
3. Establish Evaluation Criteria: Determine the criteria you will use to evaluate each solution. These criteria will make up the second dimension of your matrix.
4. Payoffs should be assigned: Assign a payout value to each intersection of a solution and a criterion in your matrix. This value should indicate the solution’s effectiveness or benefit in relation to the given criterion.

1. Examine the Matrix: Examine the finished matrix to determine which solutions have the best overall payoffs based on your criteria.
2. Consider Different Points of View: If applicable, incorporate several stakeholder perspectives into the matrix, which may change the reward values.
3. Make Informed Choices: Utilize the matrix’s findings to pick solutions that provide the greatest overall advantages.

In this context, the payoff matrix promotes an organized and comparative approach to decision-making by ensuring that all possibilities are carefully evaluated against critical criteria.

Case Study 1 – Prioritization with pay off matrix

This case study will give an example of a company trying to make its marketing decision.

Scenario: Marketing Strategy Decision

A small tech startup, ABC, is deciding on its marketing strategy for the upcoming quarter. The company is torn between two options: a digital marketing campaign (Option A) and a traditional marketing approach involving print and media ads (Option B). The effectiveness of each strategy is dependent on the market’s response, which can be either highly receptive (Scenario 1) or moderately receptive (Scenario 2).

Options:

• Option A: Digital Marketing Campaign
• Option B: Traditional Marketing Campaign

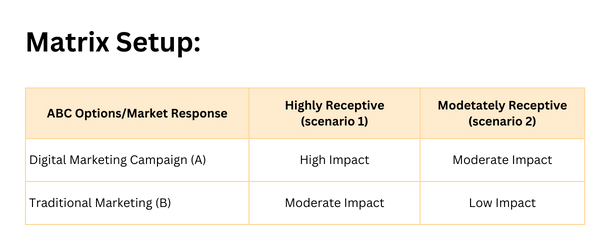
Matrix Setup:

We’ll not set up our payoff matrix:

Matrix Payoffs:

• High Impact: Substantial increase in customer engagement and sales.
• Moderate Impact: Noticeable improvement but not as significant as ‘High Impact.’
• Low Impact: Minimal improvement in engagement and sales.

Results:

If the market is highly receptive (Scenario 1), the Digital Marketing Campaign (Option A) will have a High Impact, whereas the Traditional Marketing Campaign (Option B) will only have a Moderate Impact. If the market is moderately receptive (Scenario 2), Option A still leads to a Moderate Impact, while Option B results in a Low Impact.

Based on the payoff matrix, the Digital Marketing Campaign (Option A) is the more robust strategy as it leads to at least moderate success in both scenarios. In contrast, the Traditional Marketing Campaign (Option B) risks having a low impact if the market is only moderately receptive. TechNovate, therefore, should consider prioritizing the Digital Marketing Campaign for its upcoming quarter’s strategy.

Case Study 2 – Business rivalty with pay off matrix

This case study will examine a case study between two art collectors.

Scenario: Auction Bidding

In this scenario, two rival art collectors, Alice and Bob, are bidding for a rare painting at an auction. They have two options each: bid high (Option H) or bid low (Option L). The total sum of money available for the bid is constant, and the outcome depends on their individual bidding strategies. The higher bid wins the painting, but at a higher cost, while a lower bid saves money but risks losing the painting.

Players:

1. Alice
2. Bob

Options for Each Player:

• Option H: Bid High
• Option L: Bid Low

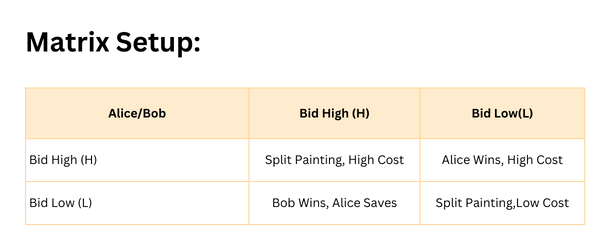
Matrix Setup:

Here’s how we can create our payoff matrix:

Matrix Payoffs:

• Split Painting, High Cost: Both players bid high, and the sum is split; both incur high costs.
• Alice Wins, High Cost: Alice bids high and wins but at a higher cost, while Bob saves his money.
• Bob Wins, Alice Saves: Bob bids high and wins, Alice saves by bidding low.
• Split Painting, Low Cost: Both bid low, neither wins the painting, but both save money.

Results:

• If both Alice and Bob Bid High (H), they split the painting but incur high costs.
• If Alice Bids High (H) and Bob Bids Low (L), Alice wins the painting at a high cost.
• Conversely, if Alice Bids Low (L) and Bob Bids High (H), Bob wins the painting, and Alice saves her money.
• If both Bid Low (L), neither wins the painting, but both save money, resulting in a split of the sum at a low cost to each.

This payoff matrix shows a classic constant sum game where the total sum remains constant, and the players’ choices directly affect their individual gains or losses.

Prioritization and Decision Making Tools

You can use prioritization or strategy making tools to ease your business decisions. You can try business strategy templates to help your operational processes.

If you’re looking for an easy-to-use solution to prioritize your daily tasks, try our priotization tools:

– This image is from Action Priority Matrix Google Sheets Template by Someka –

Yet another tool might be our decision matrix:

– This image is from Decision Matrix Google Sheets Template by Someka –

6. Payoff Matrix Wrap up

Finally, the payoff matrix is a diverse and strong tool in the strategic decision-making arsenal. Its applications span from simplifying complex game-theoretical problems such as the Prisoners’ Dilemma to assisting with daily business choices and prioritizing solutions in a variety of disciplines.

A payoff matrix’s effectiveness resides in its capacity to visually describe and compare the results of various tactics or actions, making complicated circumstances more understandable and controllable.

7. FAQ’s

We’ll try to answer most common questions on payoff matrices.

What is payoff in game theory?

A payoff is the consequence or reward that a player receives from a given action or strategy in a game. This outcome, which is frequently quantified in terms of utility, profit, or other relevant measures, is determined by the set of strategies chosen by all game players.

Payoffs are an important part of game theory because they assist players understand the consequences of their decisions and guide them in making them. Players in strategic games try to maximize their payoffs based on the strategies they and others use.

What is the payoff matrix of a market structure?

The payoff matrix of a market structure is an economic tool used to examine the results of various strategic actions made by enterprises within a specific market. It shows how the payoffs (such as profit or market share) for each firm are determined by the strategic decisions made by all enterprises in the market.

In an oligopoly market, for example, the matrix might indicate how different pricing tactics used by competing firms affect their relative payoffs. This matrix assists businesses in anticipating the potential consequences of competitive interactions and strategizing accordingly.

Recommended Readings:

How to Make Decision Matrix in Excel to Make Better Decisions?

Six Sigma Methodology: Definiton & Complete Overview About It

How to use Excel Solver for Linear Programming: Solving Optimization Problems